Las cargas o aparatos eléctricos convierten energía eléctrica en otra forma de energía útil para la aplicación, por ejemplo, un motor convierte energía eléctrica en trabajo mecánico sobre el eje del motor mismo.
Algunas cargas eléctricas utilizan campos magnéticos en su principio de funcionamiento, tales como motores, transformadores o balastos. A estas cargas se las llama cargas reactivo-inductivas y consumen parte de la energía que reciben en generar este campo magnético, necesario para que funcione, pero que no es el propósito de la aplicación.
A la parte de la energía usada para generar el campo magnético se la llama energía reactiva y se mide en kilovolt-ampere reactivo (kVAR), mientras que la otra parte que se convierte en algo útil para la aplicación se llama energía activa, y se mide en kilowatt-hora (kWh).
Si tomamos un motor y lo conectamos a la red, este tomará, por ejemplo, una corriente de 95 amperes a través de la cual transportará las energías activa y reactiva.
Por suerte, existe un componente eléctrico pasivo llamado capacitor, que al conectarse en paralelo con una de estas cargas inductivas, si se dimensiona correctamente, su presencia hace que no sea necesario entregar energía al conjunto para generar el campo magnético necesario para que la aplicación funcione.
En el caso del ejemplo del motor, si instalamos el capacitor correcto en paralelo, no será necesario que la red entregue energía reactiva, y por lo tanto la potencia sobre el eje del motor será la misma, pero ahora, por ejemplo, tomará de la red solo 65 amperes. Es decir, todo funciona igual ahorrando energía y con menos corriente. 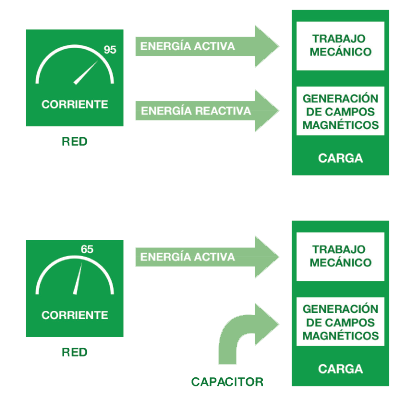 Figura 1 Figura 1
¿Qué es el factor de potencia?
Las potencias eléctricas son las velocidades con las que se transfieren las distintas energías.
Las potencias son valores instantáneos, mientras que los consumos de energía se refieren a un periodo (un mes, por ejemplo). La potencia activa (kW) es la velocidad de transferencia de la energía activa (kWh). La potencia reactiva (kVAR) es la velocidad de transferencia de la energía reactiva (kVARh). La suma vectorial de las potencias activa y reactiva de la potencia aparente (kVA), que se puede calcular fácilmente como el producto de la corriente por la tensión (por 1,73 en caso de corrientes de línea en un sistema trifásico).
Vemos en la figura 2 la representación de la suma vectorial de la potencia activa P y de la potencia reactiva Q1, que da como resultado la potencia aparente S.
Representando a la potencia reactiva capacitiva Qc del capacitor en forma opuesta la potencia reactiva inductiva de la carga Qa, vemos que la presencia del capacitor hace que la potencia reactiva, ahora del conjunto, se reduzca a Q2, provocando también una reducción de la potencia total S2.
Obsérvese que por más que se reduzca Q colocando capacitores, la potencia activa de la instalación no cambia nunca. Es decir, la carga desarrolla la misma potencia útil pero tomando mucho menos potencia aparente de la red, haciendo a la aplicación mucho más eficiente desde el punto de vista del consumo de energía.
El factor de potencia es la relación entre la potencia activa y la potencia aparente, y es un índice que indica el aprovechamiento que hace la instalación del suministro eléctrico disponible.
También se llama coseno fi (cos φ) porque su fórmula de cálculo corresponde a la relación del coseno del ángulo fi en el triángulo de potencias analizado. 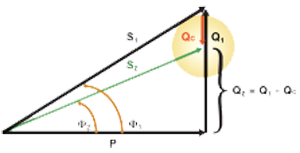 Figura 2 Figura 2
¿Qué se logra mejorando el factor de potencia?
Al mejorar el factor de potencia en una instalación eléctrica, se hace mucho más eficiente el consumo de energía, pero además se obtienen los siguientes beneficios técnicos:
-
Reducción de la generación, transporte y distribución de energía eléctrica en la red pública.
-
Aprovechamiento mayor de la capacidad interna de distribución de energía de una instalación.
-
Reducción de las pérdidas eléctricas, por reducirse la corriente necesaria para transportar la misma energía activa.
-
Mejoramiento de la calidad de energía ya que, al reducir la corriente, se reduce la caída de tensión en cables.
-
Eliminación de penalidades que se estuvieran pagando por bajo factor de potencia y, eventualmente, obtener una bonificación por buen factor de potencia.
Datos de las facturas de energía eléctrica
Los datos indicados en las facturas de energía eléctrica de cada distribuidora difieren pero, en general, todas incluyen como mínimo los siguientes:
-
P. Potencia activa (kW)
-
S. Potencia aparente (kVA)
-
ER. Energía reactiva (kVArh)
-
EA. Energía activa (kWh)
-
Tg φ1. Tg φ sin capacitores
-
Tg φ2. Tg φ deseada

 A la potencia activa también se la suele denominar como demanda y, como es un valor instantáneo, normalmente la factura indica el máximo ocurrido en el periodo. A la potencia activa también se la suele denominar como demanda y, como es un valor instantáneo, normalmente la factura indica el máximo ocurrido en el periodo.
También figuran en la factura los consumos de energía reactiva (ER) y de energía activa (EA).
Conociendo ER y EA, podemos conocer la Tg φ1, en donde el subíndice 1 indica la situación sin colocar nuevos capacitores, es decir, sin nada o con los preexistentes. Es importante saber si hay capacitores ya instalados cuando se encara un proyecto para mejorarle el factor de potencia.
La Tg φ2 corresponderá al factor de potencia o coseno fi que se desee obtener, en donde el factor de potencia mínimo a considerar es aquel fijado por la reglamentación. El subíndice 2 representa valores luego de haber aplicado la corrección con los capacitores correspondientes.
A continuación, se indica la correspondencia entre los valores de coseno y de tangente fi según reglamentación local:
-
Cos φ2 = 0,9 Tg φ2 = 0,5
-
Cos φ2 = 0,93 Tg φ2 = 0,4
-
Cos φ2 = 0,96 Tg φ2 = 0,3
-
Cos φ2 = 0,98 Tg φ2 = 0,2
-
Cos φ2 = 1 Tg φ2 = 0
Partiendo de tangente φ1 igual a energía reactiva sobre reactiva (ER/EA), y de la potencia activa P de la instalación, que se indica en kilowatts, y conociendo el factor de potencia 2 o la tangente φ2 que se desea alcanzar, se puede calcular la potencia de los capacitores necesarios usando la siguiente fórmula
Al término que resulta de sustraer la tangente φ2 de la tangente φ1 se lo denomina factor de corrección X y también se puede obtener gráficamente de la tabla de corrección. Este cálculo apenas determinará la potencia capacitiva necesaria para realizar la corrección.
Luego se deben aplicar ciertos criterios para determinar si la corrección debe ser automática, cómo debe configurarse el equipo, si este tiene que contar con algún tipo de filtrado para armónicas y, dependiendo de la velocidad de variación de la carga, puede requerir conmutación a través de tiristores (corrección dinámica).
En caso de instalaciones aún en proyecto, donde no es posible hacer mediciones ni contar con facturas de energía, se debe estimar la potencia capacitiva teniendo en cuenta la potencia activa que se instalará y el tipo de carga.
Suponiendo el caso típico de una fábrica donde la mayoría de la carga serán motores con variadores de velocidad, se puede estimar que el factor de potencia sin capacitores puede ser aproximadamente de 0,7, y para llevarlo a 0,95 se requerirá un factor de corrección de 0,7, es decir, que habría que instalar en kilovolt-amperes reactivos el setenta por ciento de los kilowatts que se vayan a instalar como carga.
Además, el equipo deberá ser automático y, por tratarse de una cantidad significativa de variadores de velocidad, se requerirá filtrado de absorción parcial de quinta armónica. |
 Figura 1
Figura 1


