En el mismo año en que Thomas Johann Seebeck (1760-1831) investigaba la termoelectricidad (hoy en día más conocida como “efecto Seebeck”), el físico británico Humphry Davy (1778-1829) había llegado a la conclusión de que la resistividad eléctrica de un metal estaba relacionada con la temperatura ambiente.

Davy pudo demostrar que la conductividad eléctrica de un metal disminuye cuando es expuesto a temperaturas crecientes, y que la resistencia medida es directamente proporcional a su longitud e inversamente proporcional a su sección transversal. Esta es la descripción básica de cómo funciona un detector de temperatura resistivo (RTD, por sus siglas en inglés).

El descubrimiento del principio que explica el funcionamiento de los RTD es solo uno de los cientos de experimentos y descubrimientos que Davy realizó durante sus cincuenta años de vida. Davy fue un brillante químico experimental, así como un físico con un gran interés en la electricidad.
Inventó la técnica de protección catódica contra la corrosión y diseñó la lámpara de Davy, la primera lámpara diseñada expresamente para su uso en minas. Esta lámpara no podía funcionar como fuente de ignición en entornos potencialmente explosivos. Y estos son solo un par de sus logros.
Nacido en el seno de una familia acomodada, Davy demostró desde muy joven una aguda inteligencia y una fascinación por el aprendizaje. Su padrino, un cirujano y boticario llamado Dr. John Tonkín, se encargó de la educación de Davy.
En 1797, después de aprender francés casi por su cuenta, leyó el "Traité élémentaire de chimie" (“Tratado elemental de Química”) de Antoine Lavoisier, un acontecimiento que definió su vida futura.
Su talento para la química fue reconocido en la activa comunidad científica que existía a principios del siglo XIX en Gran Bretaña, lo que le permitió ser elegido como uno de los primeros miembros de la Royal Society.

En la Royal Society, Davy se convertiría en un conferenciante notorio, que con frecuencia hacía uso de demostraciones químicas espectaculares y a veces peligrosas. Contaba con un estilo natural y una atractiva apariencia; estos factores, combinados con sus puntos de vista progresistas sobre el rol de las mujeres en la ciencia (estaba convencido de que las mujeres deberían tener los mismos derechos legales que los hombres, una postura que fue criticada por sus pares), le valieron el favor de las mujeres jóvenes y educadas en Gran Bretaña a principios de 1800.
Sus conferencias públicas siempre fueron muy concurridas, con la mitad de la audiencia formada por científicos y la otra mitad por mujeres que lo idolatraban. Davy era el equivalente de una estrella de rock en el siglo XIX.

Cuando estaba haciendo la investigación para este artículo, me sorprendió descubrir que la mayoría de las crónicas sobre el desarrollo de los RTD omitían cualquier mención de trabajo adicional sobre el tema hasta 1871.
Afortunadamente, pude llenar ese vacío de cincuenta años con algunas fuentes verificadas, a las cuales doy crédito al final de este artículo.
El matemático y físico Emil Khristianovich Lenz (también conocido como Heinrich Friedrich Emil) (1804-1865) nació en Estonia de padres alemanes.
Comenzó a estudiar Electromagnetismo en 1831. Aprovechando su formación en matemáticas, descubrió dos leyes fundamentales que explican la relación entre las corrientes eléctricas en las bobinas de inducción y los cambios de temperatura.
La falta de conocimientos formales sobre matemáticas fue un defecto común de muchos de los primeros pioneros de la electricidad, que normalmente eran experimentadores talentosos, pero no sobresalían en matemáticas, ya que la profunda conexión entre esta rama del conocimiento con la física y la química aún estaba en desarrollo. De hecho, esta fue la razón por la que Michael Faraday (1791-1867) tuvo que convocar a James Clark Maxwell (1831-1879) para realizar los desarrollos matemáticos incluidos en su trabajo clásico sobre el electromagnetismo.

Es posible que recuerde la ley de Lenz y sus pequeñas consecuencias.
Emil Lenz formuló la ley de la electrodinámica que lleva su nombre, la cual descubrió mientras experimentaba con bobinas hechas de diferentes metales e imanes permanentes.
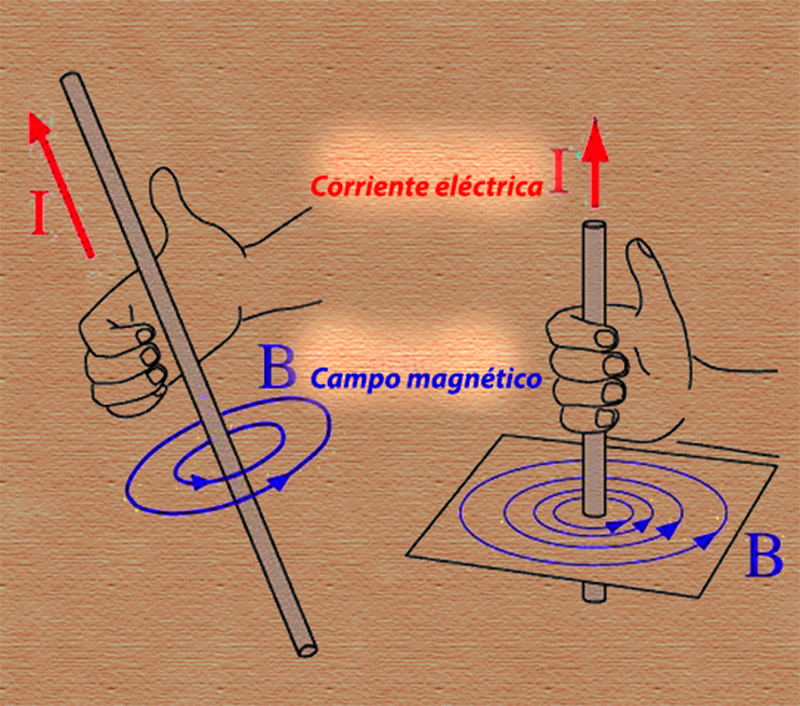
La ley de Lenz establece que, cuando pasa un imán a través de una bobina metálica, se crea una corriente eléctrica en la bobina. La dirección de esa corriente depende de la dirección de los polos magnéticos del imán permanente. Si el lector alguna vez ha estudiado electromagnetismo, probablemente recordará la ley de Lenz como la "regla de la mano derecha", utilizada para determinar la dirección de un campo magnético creado por una corriente.
Pero antes de este descubrimiento, Lenz trabajó en el estudio de la conductividad eléctrica y la resistencia en varios tipos de metales.
Terminó creando un circuito con una fuerza electromotriz sin la resistencia interna de una batería y descubrió que la resistencia eléctrica de un metal variaba a diferentes temperaturas.
Además, creó fórmulas empíricas que permitían calcular la conductividad de metales específicos a diferentes temperaturas. También determinó los rangos de temperatura en los que se podían usar sus fórmulas.
Estos resultados fueron verificados diez años más tarde por el físico y matemático alemán Johann Heinrich Müller (1809-1875).
Una consecuencia de este trabajo de investigación fue su descubrimiento independiente de la relación matemática entre la potencia, la corriente y la resistencia en un conductor eléctrico, es decir, la ley de Joule. Esta es la razón por la que en Rusia la ley de Joule se conoce como la “ley de Joule-Lenz”.

[1] P = I (V_a-V_b)

donde ‘V_a-V_b’ es la caída de voltaje en el circuito, por lo tanto:

[2] P = I V

Y si combinamos esto con la ley de Ohm (‘V = I R’) entonces:

[3] P = I V = I² R = V²/R

Las fórmulas y los resultados de Lenz fueron mejorados por el físico francés Alexandre Edmond Becquerel (1820-1891) aunque este no reconoció sus fuentes. Utilizando nuevos aparatos disponibles, Becquerel llegó a la conclusión de que el aumento de la resistencia por un cambio unitario de temperatura (dr/dt) era una constante característica para cada metal estudiado. Esta constante o coeficiente del incremento de la resistencia es el valor "a" en la fórmula de Becquerel:

[4] R = R₀ (1 + at)

donde ‘R₀’ es la resistencia del metal a 0 °C.

La fórmula de Becquerel fue mejorada por el trabajo de un astrónomo y físico irlandés, el reverendo Dr. Thomas Romney Robinson (1792-1882), quien introdujo un factor de corrección en la fórmula para corregir las variaciones debidas a la expansión del cable a medida que aumentaba la temperatura.

[5] R= R_o + b T

donde ‘b’ era el cambio de resistencia por un grado.

La fórmula final presentada por Robinson fue:

[6] R = R_o + b T - c R² I²

Los valores ‘a’, ‘b’ y ‘c’ eran específicos para cada sustancia y debían determinarse empíricamente. Robinson hizo todos estos experimentos utilizando alambres de platino. El uso de otros metales presentaba problemas debido a que la expansión de su alambre era difícil de medir con la tecnología disponible en ese momento.
Los bajos niveles de pureza de los alambres metálicos disponibles en ese tiempo generaban niveles inaceptables de incertidumbre en los intentos de utilizar el fenómeno descubierto por Humphry Davy en 1821 con fines prácticos.
La historia del desarrollo de los RTD está conectada con los cambios que la Revolución Industrial produjo, primero en Europa, y después en el resto del mundo. Curiosamente, la investigación de las telecomunicaciones se volvió fundamental para el establecimiento de los RTD como el método preferido para la medición de temperatura de alta precisión. Pero discutiremos eso en la siguiente parte de esta serie de artículos.

El vacío de cincuenta años en la historia de los RTDI se completó con datos obtenidos de un artículo publicado en la Revista Brasileira de Ensino de Física, v. 33, n. 4, 4602 (2011) www.sbfisica.org.br
El título del artículo es: "Estudios sobre la dependencia de la temperatura de la conductividad eléctrica para metales en el siglo XIX: un capítulo olvidado en la historia de la superconductividad".
El autor es Simón Reif-Acherman, quien en ese momento se encontraba en la Escuela de Ingeniería Química de la Universidad del Valle, Cali, Colombia.
Si se está preguntando qué relación existe entre la invención de la RTD y el descubrimiento de la superconductividad, la respuesta es la siguiente: la resistividad de un metal aumenta proporcionalmente con la temperatura. Pero también podríamos decir que la conductividad de un metal aumenta cuando la temperatura disminuye. Por lo tanto, la posible consecuencia de este comportamiento de los metales sería que, si la temperatura del metal es cercana a 0 °K, su conductividad derivaría hasta el infinito (o su resistividad estaría tan cerca de cero como podríamos bajar la temperatura del ambiente).
Y este hecho se puede derivar de las ecuaciones que C. W. Siemens creó para describir la relación de ‘R’ y ‘T’ en metales altamente conductores.
Inicialmente:

[7] R_(t) = α T₁/2

donde α es un coeficiente específico de cada metal

Pero esta fórmula no puede describir el aumento de R debido a la expansión del metal debido al calor. Así que Siemens especuló que un segundo término con la forma β x T funcionaría, siendo β un coeficiente relacionado con la expansión del metal cuando se expone a temperaturas más altas y con un γ constante que indicaría la resistencia a un cero absoluto teórico (las escalas de temperatura absoluta se crearon un poco más tarde). Por lo tanto, C.W. Siemens especuló que esto podría modelarse utilizando la siguiente ecuación:

[8] R_(t) = α T₁/2 + β T + γ

donde ‘α’, ‘β’ y ‘γ’ serían coeficientes específicos de cada metal. γ sería la resistividad de un metal en el cero absoluto, evitando así la aparición de singularidades de la conductividad infinita o la resistividad nula en condiciones de cero absoluto. Y estas son las condiciones extremas que permiten que una substancia se comporte como un súper conductor.