En el presente trabajo se abordan dos problemas principalmente: el modelizado y control de un aerogenerador con sistema de pitch, y la comunicación de los datos obtenidos en Simulink en tiempo real por medio de un simulador de OPC DA server.
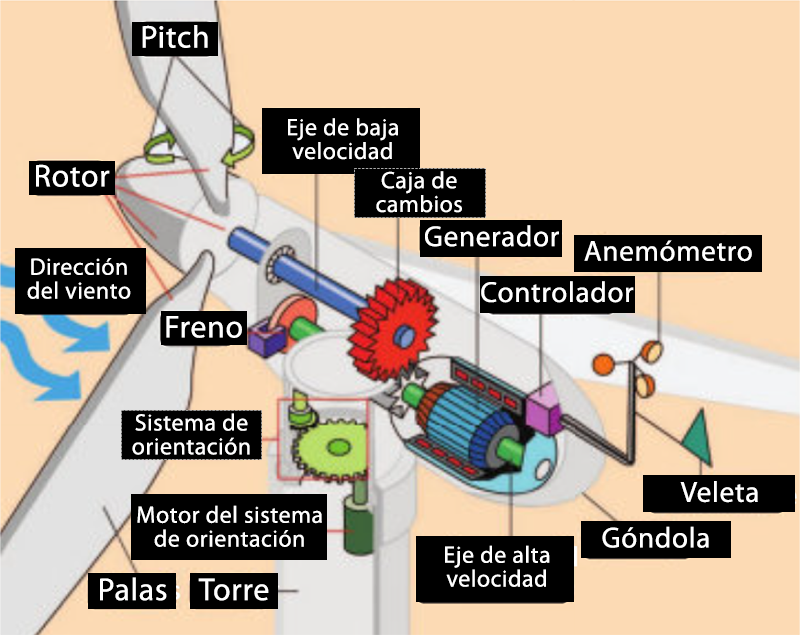
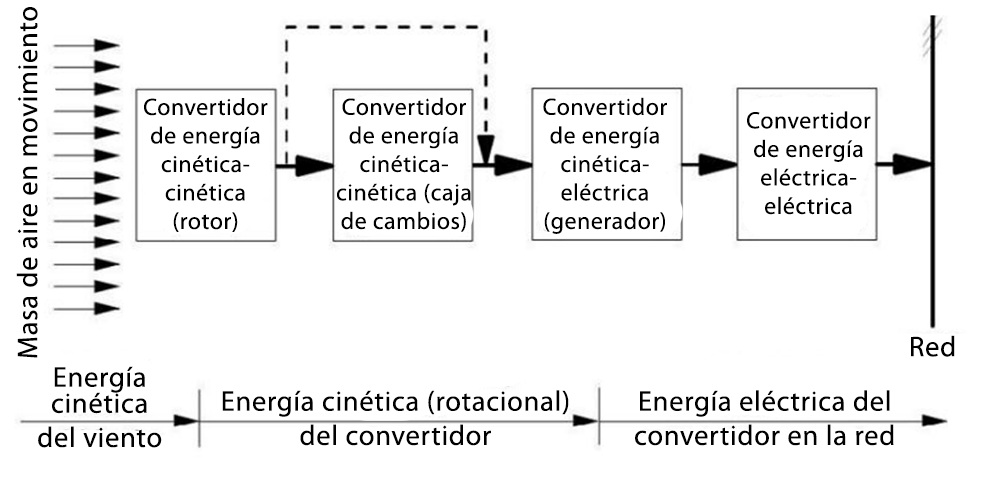
En el presente trabajo se abordan dos problemas principalmente: el modelizado y control de un aerogenerador con sistema de pitch, y la comunicación de los datos obtenidos en Simulink en tiempo real por medio de un simulador de OPC DA server. A fin de entender más sobre estos sistemas, resulta conveniente entender qué hacen estas máquinas e identificar las partes principales de un aerogenerador, tal como se visualizan en la figura 1. Además, conviene entender las conversiones de energía descriptas en la figura 2.
El sistema de pitch o de orientación de las palas les permite a los aerogeneradores mantener las revoluciones en un rango de operación que permite la máxima absorción de energía cinética del viento, además de favorecerlos desde un punto de vista estructural. Cuando giran las palas del aerogenerador sobre su eje, la máquina puede adoptar distintas propiedades aerodinámicas que hacen que la conversión de desplazamiento axial del viento se transforme en movimiento rotacional del rotor en mayor o menor medida. De esta forma se puede evitar el embalamiento del rotor y se puede aprovechar un mayor rango de velocidades de operación.
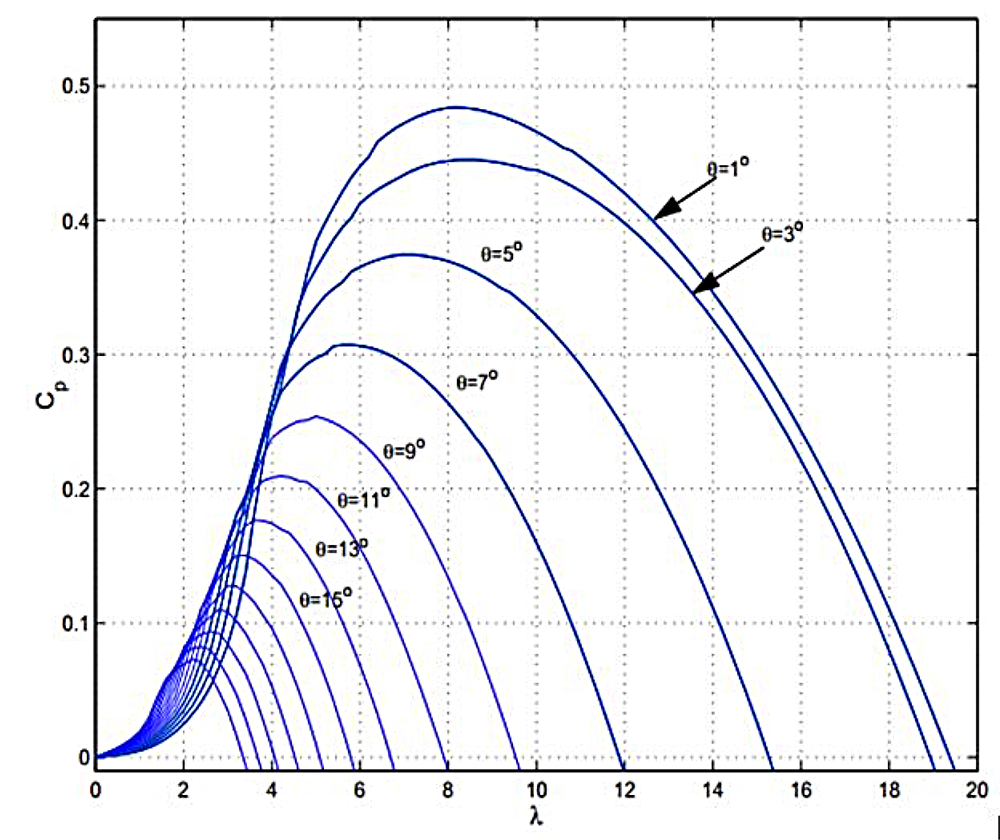
A fin de entender la importancia de este sistema que suele pasar desapercibido en estos gigantes, se presenta en la figura 3 el dramático efecto que tiene una pequeña variación en el ángulo de las palas respecto al viento para una máquina de 60 kW.
A fin de entender la importancia de este sistema que suele pasar desapercibido en estos gigantes, se presenta en la figura 3 el dramático efecto que tiene una pequeña variación en el ángulo de las palas respecto al viento para una máquina de 60 kW.
Algoritmo de control propuesto
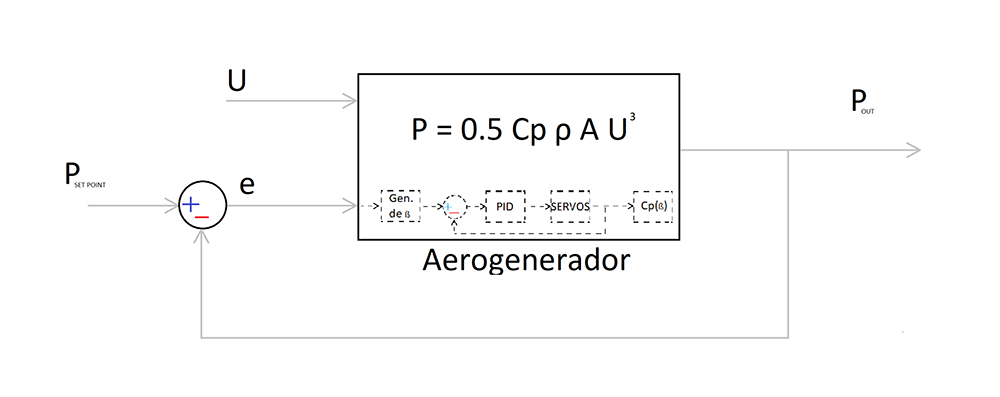
En un principio se planteó un sistema de control con un PID que, una vez llegado al punto de ajuste, comience a actuar en el ángulo de ataque de las palas de manera de mantener una generación de potencia lo más estable y constante posible. ‘U’ es la velocidad del viento, ‘Pset point’ es la potencia que se debe mantener y ‘Pout’ es la potencia que está entregando la máquina. A su vez, está el lazo en cascada del sistema pitch, donde se solicita un ángulo en los actuadores en función del error del lazo principal gobernado por la ecuación 1.
(1) P = 1/2 CpρAU3
En la ecuación (1) se ve que la potencia absorbida depende del área descrita por la rotación de las palas ‘A’, la velocidad del viento ‘U’, lu densidad ‘ρ’ y la relación ‘Cp’ entre la potencia absorbida del viento y la disponible, que teóricamente no puede superar el 59%, aproximadamente.
Diagrama de bloques en Simulink
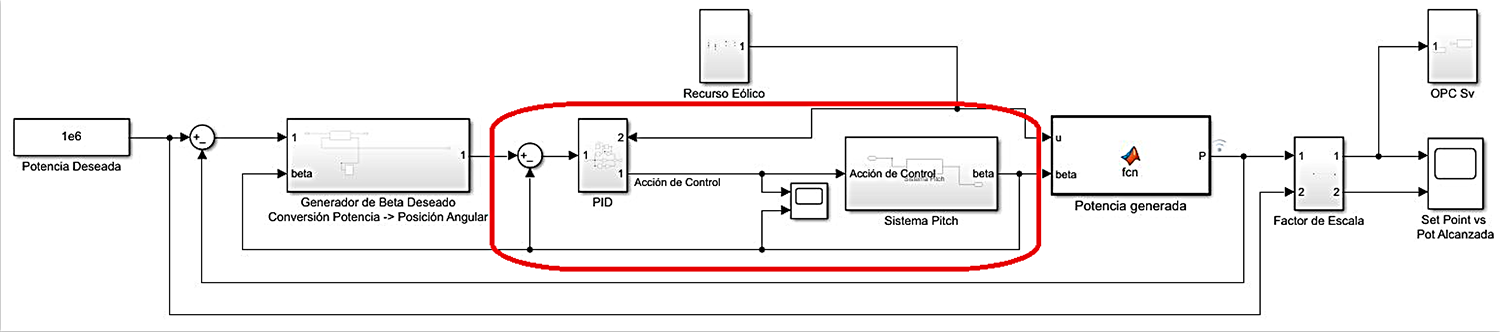
En Simulink se plantea el diagrama de la figura 5, donde se puede identificar el lazo lento y el lazo rápido con rojo, que es el posicionamiento del ángulo de las palas respecto al viento. Por otro lado, se ve el subsistema denominado “Recurso eólico”, encargado de generar viento según una distribución de Weibull que se puede adaptar a cualquier región de interés dados los factores de escala y forma que definen la distribución de esta función densidad de probabilidad.
Entradas y salidas del sistema
Viento generado
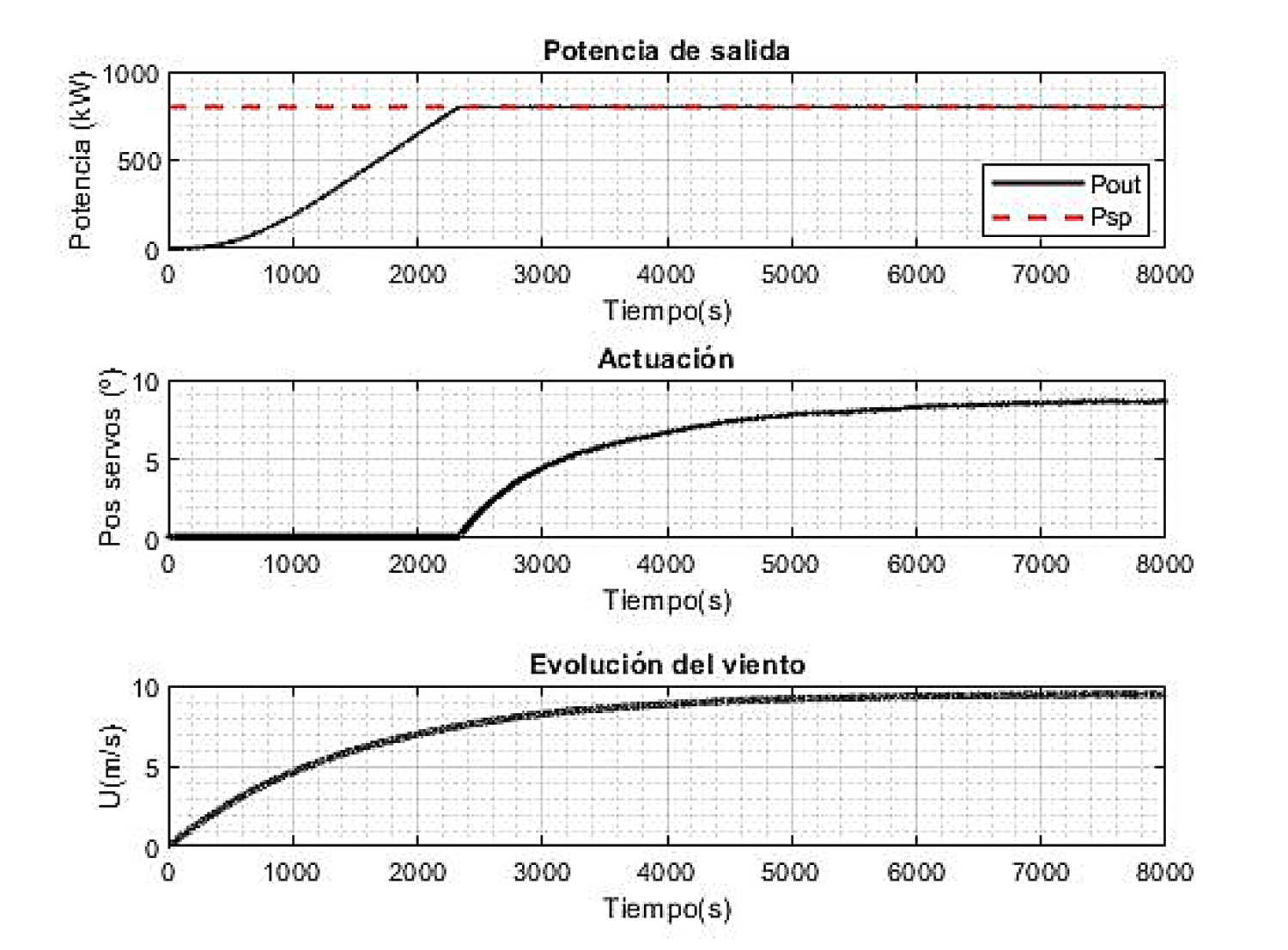
El subsistema recurso eólico entrega la entrada al sistema (ver tercer gráfico de la figura 8). A fin de definir los valores entregados, se cargan un factor de forma y escala, según el cual se generan valores aleatorios de acuerdo a una distribución de Weibull. Luego de este bloque, se coloca un filtro con el objetivo de obtener valores que adopten una dinámica similar a la que seguiría esta planta.
Modelo del actuador
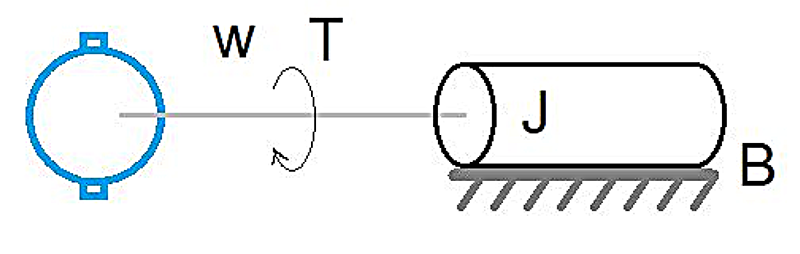
Se modelizan los actuadores con la siguiente función transferencia:
(2) [θ(s) / T(s)] = {1 / [Js2θ(s) + Bsθ(s)]}
La salida será la posición del servomotor ‘θ’ y la entrada, el torque resultante ‘T’; ‘J’ es la inercia de la carga y ‘B’, el coeficiente de rozamiento.
Se diseña un PID en el lazo rápido o anidado, y se obtiene así la respuesta observada en el segundo gráfico de la figura 8.
Se diseña un PID en el lazo rápido o anidado, y se obtiene así la respuesta observada en el segundo gráfico de la figura 8.
Modelo de la planta
En esta ocasión se busca una relación sencilla entre el cociente de las revoluciones del rotor y la velocidad axial del viento ‘λ’, y la relación ‘Cp‘ de la máquina, que es lo que define su curva de rendimiento.
La familia de curvas queda definida por el posicionamiento de los actuadores, en un rango de valores que va desde 1 hasta los 15°. Se verifica que con la ecuación (1); la velocidad del viento ‘U’, obtenida con un anemómetro con su dinámica; el área de barrido ‘A’, que depende principalmente de la longitud de las palas ‘R’ y es constante; la densidad del viento ‘ρ’, también constante, y el cálculo con estas curvas a fin de obtener la relación ‘Cp’, se puede finalmente calcular la potencia de salida ‘P’, que es la ley que gobierna el control en este caso. Cabe destacar que la velocidad de rotación del eje ‘ω’ puede obtenerse con un tacómetro.
Calcular ‘λ’ basta con realizar la ecuación (3):
La familia de curvas queda definida por el posicionamiento de los actuadores, en un rango de valores que va desde 1 hasta los 15°. Se verifica que con la ecuación (1); la velocidad del viento ‘U’, obtenida con un anemómetro con su dinámica; el área de barrido ‘A’, que depende principalmente de la longitud de las palas ‘R’ y es constante; la densidad del viento ‘ρ’, también constante, y el cálculo con estas curvas a fin de obtener la relación ‘Cp’, se puede finalmente calcular la potencia de salida ‘P’, que es la ley que gobierna el control en este caso. Cabe destacar que la velocidad de rotación del eje ‘ω’ puede obtenerse con un tacómetro.
Calcular ‘λ’ basta con realizar la ecuación (3):
(3) λ = ωR / U
Resultados obtenidos
Tras simular el diagrama de bloques de la figura 5, se obtiene la respuesta del sistema. Este evoluciona en una función cúbica hasta alcanzar su valor máximo según la velocidad del viento. Cuando varía la velocidad del viento, el controlador ajusta la ganancia derivativa y alcanza el nuevo régimen, hasta llegar al punto de ajuste.
Cuando el sistema llega a su valor máximo y el viento está por encima de 8,5 m/s, entonces el sistema alcanza la zona de control. En este momento se genera una señal de control con la posterior actuación de los servomotores que variarán el ángulo de ataque del aerogenerador.
Cuando el sistema llega a su valor máximo y el viento está por encima de 8,5 m/s, entonces el sistema alcanza la zona de control. En este momento se genera una señal de control con la posterior actuación de los servomotores que variarán el ángulo de ataque del aerogenerador.
Cuando varía la velocidad del viento, el controlador ajusta la ganancia derivativa y alcanza el nuevo régimen, hasta llegar al punto de ajuste
Respecto a los actuadores, se observa que no se llega a los 9°. Si se analiza la figura 7, es posible ubicar la curva de rendimiento de esta planta, y a partir de ella obtener el rendimiento de la máquina según una velocidad de viento dada. Esto, nuevamente, se puede corroborar con la ecuación (1) de la ley de control. Vale dar cuenta de que se podría obtener mayores potencias de esta planta si el punto de ajuste fuera más elevado, aunque también hay que contemplar la velocidad angular ‘ω’ para que el sistema no se embale.
Una manera alternativa de obtener la velocidad puede ser a través de un tacómetro o utilizando la ecuación (4), dados la potencia ‘P’ y el torque ‘T’, que es la entrada al sistema de pitch [ver función transferencia (2)]
Una manera alternativa de obtener la velocidad puede ser a través de un tacómetro o utilizando la ecuación (4), dados la potencia ‘P’ y el torque ‘T’, que es la entrada al sistema de pitch [ver función transferencia (2)]
(4) ω = P / T
OPC Server
Por último, y no menos importante, se busca plantar las bases de futuros desarrollos, en los que el autor de este escrito ya se encuentra trabajando. Se configura Simulink con el objeto de dar con una simulación en tiempo real, además de comunicar estos datos con el simulador de OPC DA Server de Matrikon. Con esta arquitectura se puede comunicar este sistema con un SCADA.
Se configura Simulink con el objeto de dar con una simulación en tiempo real, además de comunicar estos datos con el simulador de OPC DA Server de Matrikon
Datos en tiempo real
Tras realizar las configuraciones en Simulink y el simulador Matrikon, se verifica que se tienen datos en tiempo real.
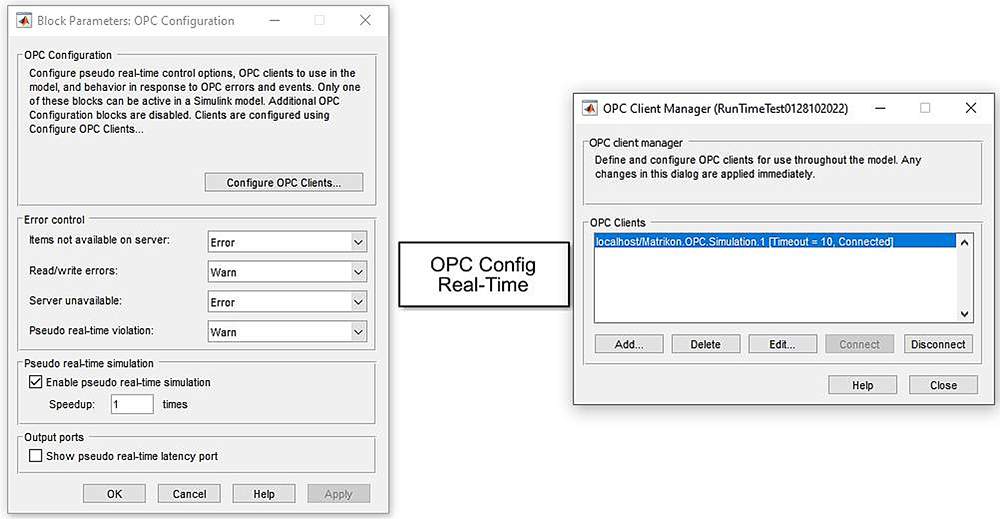
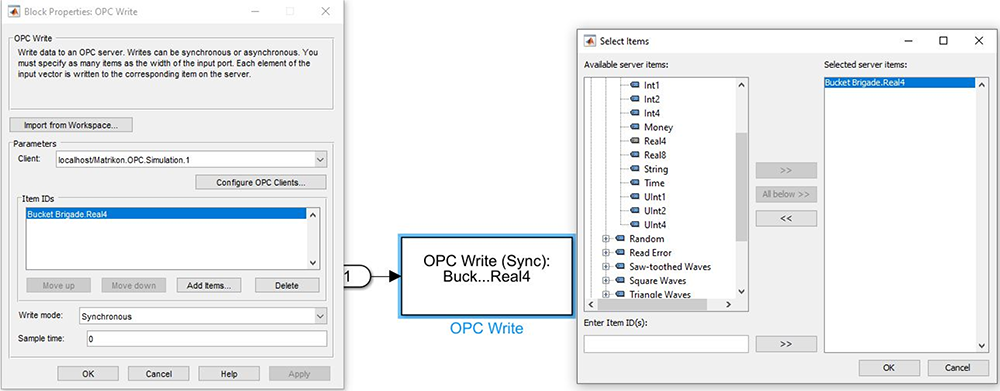
A fin de conseguir estos resultados, se utilizan los bloques OPC W rite y OPC Config Real Time. Estos bloques se encuentran en el subsistema OPC Sv a la derecha del diagrama de la figura 5.
A fin de conseguir estos resultados, se utilizan los bloques OPC W rite y OPC Config Real Time. Estos bloques se encuentran en el subsistema OPC Sv a la derecha del diagrama de la figura 5.
Configuración de los bloques
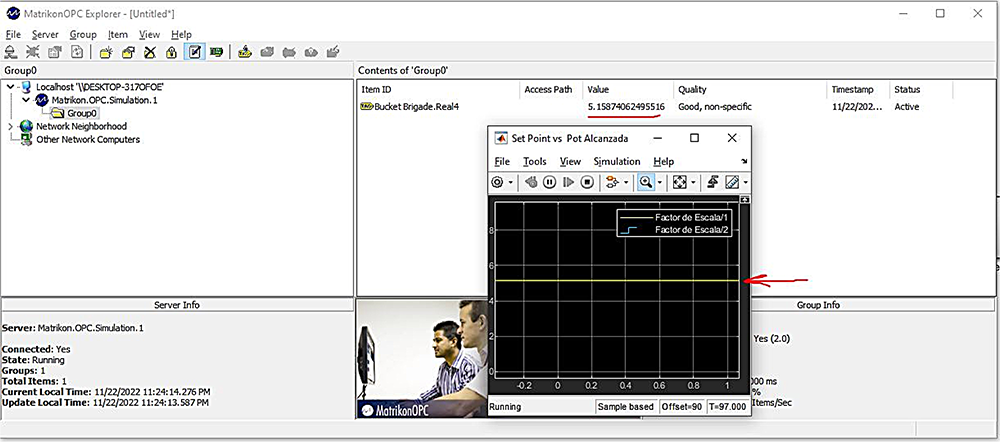
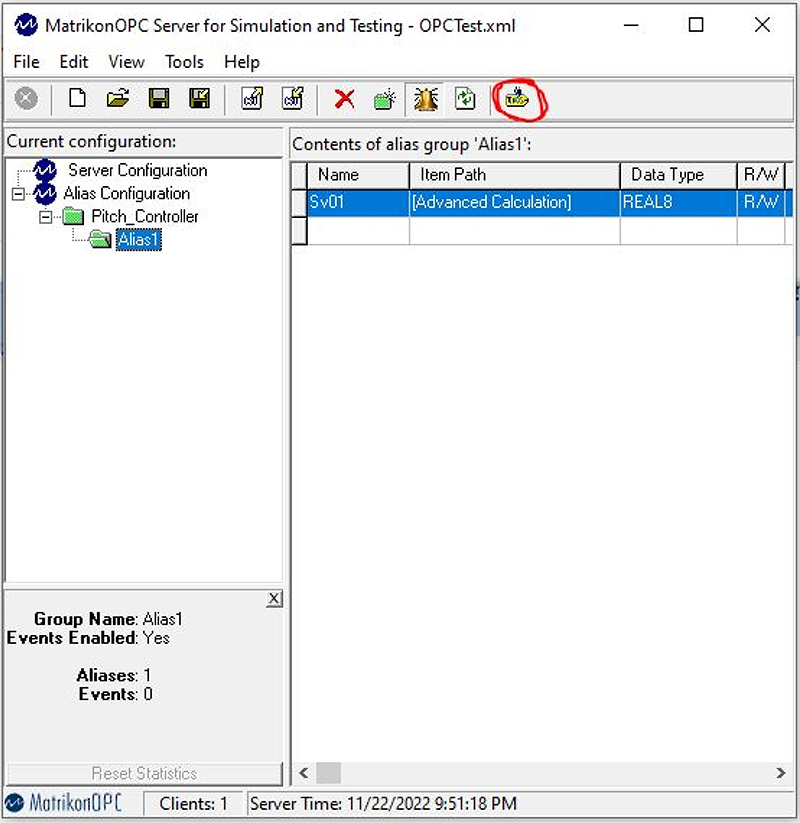
Se procede con las configuraciones de los bloques según las figuras 11 y 12. Finalmente, se crea un servidor OPC en el simulador (figura 13).
Tras finalizar estas configuraciones, se puede simular el sistema en Simulink y verificar que los parámetros que se ven en Simulink figuran de igual manera en las variables del simulador OPC (ver figura 9).
Tras finalizar estas configuraciones, se puede simular el sistema en Simulink y verificar que los parámetros que se ven en Simulink figuran de igual manera en las variables del simulador OPC (ver figura 9).
Conclusiones
Respecto a los beneficios que se obtienen con la aplicación de estos sistemas, se puede incluir incrementos en la seguridad y fiabilidad, y también en un ahorro de dinero. Esto es, el sistema de frenos que pudiera tener la máquina se complementa con el sistema pitch, y se puede operar con un sistema u otro a fin de reducir las revoluciones.
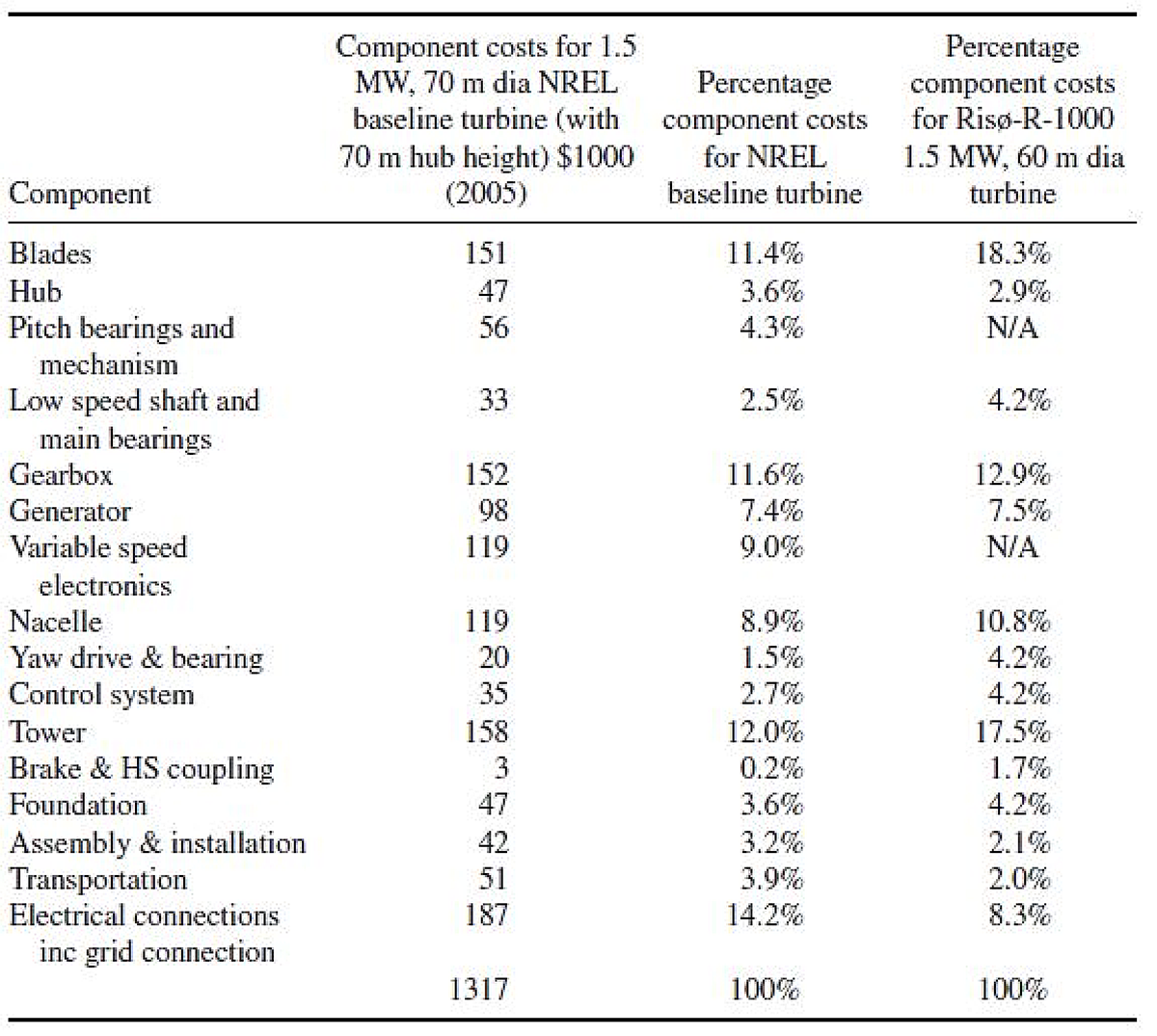
Por otro lado, se obtienen mejoras en materia de eficiencia, porque la rápida adaptación de las palas permite absorber mayor cantidad de energía más rápidamente y sin desperdicios. Se ahorra en materiales, ya que los esfuerzos en las palas serán menores en este tipo de sistemas que en aquellos que no cuentan con esto. El costo de las palas llega a ascender hasta el 11 al 18% del costo total de la máquina, por lo que se estaría ahorrando en el componente más costoso. Se puede verificar esto: se comparte un modelo de costeo de estas máquinas. Finalmente se logró establecer comunicación con un OPC DA server, posibilitando la futura comunicación con un sistema SCADA moderno.
Por otro lado, se obtienen mejoras en materia de eficiencia, porque la rápida adaptación de las palas permite absorber mayor cantidad de energía más rápidamente y sin desperdicios. Se ahorra en materiales, ya que los esfuerzos en las palas serán menores en este tipo de sistemas que en aquellos que no cuentan con esto. El costo de las palas llega a ascender hasta el 11 al 18% del costo total de la máquina, por lo que se estaría ahorrando en el componente más costoso. Se puede verificar esto: se comparte un modelo de costeo de estas máquinas. Finalmente se logró establecer comunicación con un OPC DA server, posibilitando la futura comunicación con un sistema SCADA moderno.
La rápida adaptación de las palas permite absorber mayor cantidad de energía más rápidamente y sin desperdicios
Por Pablo Nüesch, FIUBA
Referencias
[1] Andreas Wiese, Martin Kaltschmitt, Wolfgang Streicher. Renewable Energy. Springer, Alemania, 2007.
[2] Andrés Adán Ramírez. Modelo de sistema de control de paso de pala aplicado a turbina eólica. Proyecto fin de grado, Universidad Politécnica de Madrid, 2016.
[3] David Sharpe Ervin Bossany Tony Burton, Nick Jenkins. Wind Energy Handbook. Wiley, Reino Unido, 2 edition, 2011.
[4] L. Y.-. Pao y K. E. Jhonson. Control of wind turbines: Apporaches, challenges and recent developments. IEEE Control Systems Magazine, 2011.
[1] Andreas Wiese, Martin Kaltschmitt, Wolfgang Streicher. Renewable Energy. Springer, Alemania, 2007.
[2] Andrés Adán Ramírez. Modelo de sistema de control de paso de pala aplicado a turbina eólica. Proyecto fin de grado, Universidad Politécnica de Madrid, 2016.
[3] David Sharpe Ervin Bossany Tony Burton, Nick Jenkins. Wind Energy Handbook. Wiley, Reino Unido, 2 edition, 2011.
[4] L. Y.-. Pao y K. E. Jhonson. Control of wind turbines: Apporaches, challenges and recent developments. IEEE Control Systems Magazine, 2011.
Nota del editor
El presente artículo es el resumen de la tesis con la que el autor se graduó de la “Maestría en Automatización Industrial” de la Escuela de Graduados en Ingeniería Electrónica y Telecomunicaciones de la Facultad de Ingeniería de la Universidad de Buenos Aires, enfocada en la aplicación práctica de las metodologías estudiadas en las clases.
El presente artículo es el resumen de la tesis con la que el autor se graduó de la “Maestría en Automatización Industrial” de la Escuela de Graduados en Ingeniería Electrónica y Telecomunicaciones de la Facultad de Ingeniería de la Universidad de Buenos Aires, enfocada en la aplicación práctica de las metodologías estudiadas en las clases.
Autor:
Publicado en:
Número:
Mes:
Año: