Nota técnica | Detección de fallas en reductores de velocidad impulsados por motores de inducción

Carlos Verucchi, Matías Librandi, Nicolás Keesler, Matías Meira y Cristian Ruschetti
Grupo de investigación INTELYMEC, Facultad de Ingeniería de Olavarría, Universidad Nacional del Centro de la Provincia de Buenos Aires – CONICET

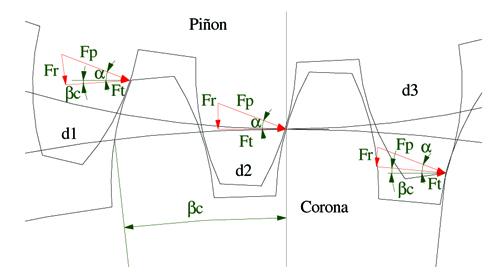
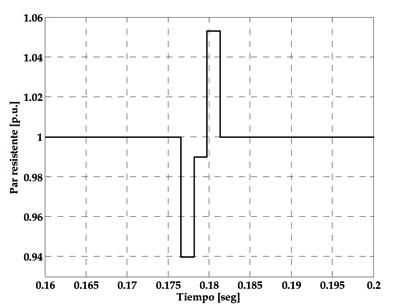
Resumen

Durante las últimas décadas se ha avanzado en el desarrollo de técnicas no invasivas de detección de fallas en motores de inducción. Como complemento a estos adelantos, se ha notado la posibilidad de detectar, a través de la medición de las variables eléctricas del motor, fallas en reductores de velocidad o anomalías en la carga accionada que podrían deberse al funcionamiento defectuoso de alguno de sus componentes.
En este trabajo se estudia la posibilidad de detectar fallas en dientes de engranajes a partir del seguimiento del par eléctrico del motor. El par eléctrico es estimado en función de las corrientes y tensiones de estator. Se propone un modelo matemático simple que permite incluir la falla de uno o más dientes en uno de los engranajes de un reductor de velocidad y se analiza mediante simulaciones computacionales el modo en que la falla incide sobre el par eléctrico del motor. Se obtienen conclusiones sobre la eficacia de la técnica de diagnóstico empleada.

Palabras clave

Detección y diagnóstico de fallas, fallas en engranajes, estimador de par.

1. Introducción

Los motores de inducción trifásicos de jaula de ardilla están presentes en la inmensa mayoría de los accionamientos empleados en procesos industriales. Su bajo costo y robustez los convierten en una alternativa prácticamente excluyente para dicho tipo de aplicaciones. Si bien estos motores presentan una probabilidad de falla mucho menor a la de otros tipos de máquinas, los altos costos asociados a paradas imprevistas en líneas de producción han forzado el desarrollo de una gran variedad de técnicas de detección temprana de fallas.
Las primeras herramientas para la detección de fallas en máquinas eléctricas estuvieron basadas en la medición de vibraciones. El estado del sistema aislante, por su parte, puede analizarse a partir de técnicas basadas en la medición de la tangente de delta o de descargas parciales. Todas estas técnicas, llamadas comúnmente tradicionales, requieren de la instalación de sensores sobre el motor (vibraciones), o bien solo son aplicables en motores fuera de servicio (tangente de delta, descargas parciales). Si bien todas ellas son de uso corriente en la actualidad, han sido recientemente complementadas con otras técnicas que presentan características no-invasivas y permiten una aplicación online. La característica más importante de ellas es que pueden ser aplicadas de manera permanente y sin interferir con el funcionamiento del motor, de ahí su denominación de no-invasivas. Así, un importante número de alternativas ha sido presentado en la literatura con el fin de detectar cortocircuitos en bobinados de estator, barras del rotor fisuradas o cortadas, excentricidades en el eje y fallas en rodamientos, entre otras. Las propuestas más destacadas, en este sentido, giran en torno al análisis del espectro de frecuencia de la corriente de estator, al seguimiento del par eléctrico estimado, a la monitorización del flujo axial del motor, de la impedancia de secuencia inversa y del vector de Park, entre otras.
Las virtudes de las nuevas técnicas de diagnóstico basadas en métodos online han sido ampliamente comprobadas en la detección de fallas en motores de inducción. Posteriormente se observó que algunas irregularidades en la carga accionada, tales como fallas en compresores o cavitación en sistemas hidráulicos, entre otras, podían ser asimismo detectadas a partir del seguimiento de las variables eléctricas del motor. Esto se debe a que el par eléctrico del motor de inducción, y por consiguiente la corriente de estator, deben adaptarse al par resistente ofrecido por la carga accionada. Por ende, una variación regular del par resistente, ocasionada por un funcionamiento incorrecto de la carga, puede ser detectada y analizada a través del motor.
A partir del argumento anterior puede concluirse, asimismo, que una irregularidad en el sistema de transmisión entre motor y carga (por ejemplo, un tren de engranajes) también incidirá sobre las variables eléctricas del motor. En efecto, ante un desgaste o rotura en un diente de un engranaje, que impida su correcto engrane con la rueda complementaria, el par necesario para mantener equilibrado el par resistente de la carga sufrirá una perturbación. Por consiguiente, analizando el comportamiento del par eléctrico estimando podría diagnosticarse una falla de esta naturaleza.
En virtud del grado de desarrollo que han alcanzado las distintas técnicas de detección de fallas en máquinas de inducción, se considera posible avanzar hacia el desarrollo de estrategias de diagnóstico que engloben fallas producidas en el motor, en la transmisión y en la carga. Si bien la bibliografía actual sobre el tema no es abundante, algunos estudios permiten vislumbrar posibilidades interesantes en este sentido.
El propósito de este trabajo consiste en desarrollar un modelo matemático simple que permita simular el comportamiento de un par de engranajes en los que un diente presenta cierto desgaste en su flanco. El modelo, si bien solo es aproximado, es de fácil adaptación a cualquier par de ruedas dentadas, independientemente de la cantidad de dientes en contacto simultáneamente, de la relación de transmisión y de la velocidad de giro. El modelo propuesto constituye una herramienta útil para la evaluación y comparación de distintas técnicas de diagnóstico de fallas.
En la sección 2 se desarrolla el modelo mecánico de la transmisión para la condición de falla. En la sección 3, se presenta el modelo de máquina de inducción utilizado para las simulaciones y el estimador de par eléctrico. En la sección 4 se muestra un ejemplo de aplicación y en la sección 5, finalmente, se presentan algunas conclusiones extraídas del trabajo.

Figura 1. Descomposición de las fuerzas de ataque sobre una transmisión entre piñón y corona con tres dientes en contacto

2. Modelo de transmisión por engranajes con falla en un diente

Para estudiar técnicas de detección de fallas en trenes de engranajes, se considera necesario contar con un modelo que permita predecir el comportamiento del conjunto formado por motor-reductor-carga ante una anomalía en uno de los dientes en el reductor. Para ello se parte de la hipótesis de que la rotura o el desgaste de un diente, tanto del piñón como de la corona, introduce una perturbación en el par que el piñón transmite sobre esta última. En efecto, la ausencia o desgaste de un diente exigirá que los otros dientes del piñon que se hallan en contacto con la corona modifiquen su fuerza de contacto para compensar los cambios que se producen en el sistema de fuerzas tangenciales sobre los dientes.
El modelo se desarrolla para el caso que existan tres dientes del piñón simultáneamente en contacto con la corona. La adaptación del modelo para un número distinto de dientes en contacto es simple.
En la figura 1 se presenta esquemáticamente el sistema a estudiar. Las fuerzas de presión Fp sobre los dientes de la corona se consideran iguales e inclinadas un ángulo α de 20 grados respecto a la horizontal (este ángulo de presión queda establecido por la geometría de la fresa con la que se talla el diente y, actualmente, se usa de manera practicamente universal un valor de 20°). Estas fuerzas se descomponen, en cada uno de los dientes, en una componente tangencial a la circunferencia primitiva de la corona (Ft) y una componente en la dirección radial (Fr). Solo la primera de estas componentes contribuye al par aplicado sobre la corona. Las componentes radiales, por su parte, constituyen un esfuerzo sobre el eje de la corona pero no contribuyen con el par transmitido dado que su radio de giro respecto al eje de rotación es cero.
Dado que las fuerzas de presión se consideran iguales en cada diente, las componentes tangenciales vienen dadas en cada caso en función del ángulo de presión (α) y del ángulo entre la tangente al diámetro primitivo y la horizontal (βc). De acuerdo con el esquema de la figura 1, este ángulo coincide con el ángulo de paso entre dos dientes consecutivos de la corona, esto es:

(1) βc = 360°/zc

donde zc es el número de dientes de la corona. El par transmitido a la corona, por consiguiente, estará dado por el aporte de las tres fuerzas tangenciales, esto es:

(2) Tc = FpRc [cos (α + βc) + cos (α) + cos (α − βc)]

donde Rc es el radio primitivo de la corona. Se desprende de la figura 1 que en realidad el radio de aplicación de las fuerzas sobre cada diente no es exactamente Rc. En efecto, solo la fuerza aplicada por el diente 2 del piñón actúa sobre la corona exactamente con un radio Rc. Sin embargo, si se considera que generalmente el alto de un diente es mucho menor al radio de la rueda dentada, las diferencias en los radios de aplicación de las fuerzas de cada diente pueden despreciarse. De tal modo, con fines de simplificación, se toma Rc como la distancia de aplicación de las fuerzas sobre cualquier diente.

Figura 2. Variación temporal de par resistente visto desde el motor para el caso de un diente defectuoso de acuerdo al modelo presentado.

Para considerar un caso de falla, se supone que el diente 1 del piñón (figura 1) presenta desgaste en su flanco o bien rotura y por lo tanto no ejerce presión sobre la corona. Dado que el par resistente de la carga se considera constante, ante esta situación, la ecuación 2 deberá reescribirse sin el término que corresponde al diente d1 e igualarse al mismo par Tc dado para condición libre de falla.

(3) Tc = Fp_falla Rc[0 + cos (α) + cos (α − βc)]

donde Fp_falla es la nueva fuerza de presión para el caso de falla. De la ecuaciones 2 y 3 es posible deducir la relación entre las fuerzas de presión entre dientes para las condiciones con y sin falla:
(4) Fp_falla/Fp = [cos (α + βc) + cos (α) + cos (α − βc)] / [0 + cos (α) + cos (α − βc)]

Por otra parte, escribiendo la ecuación 2 aplicada al piñón resulta:

(5) Tp = FpRp [cos (α - βp) + cos (α) + cos (α + βp)]

donde Tp es el par sobre el piñón y βp es el ángulo entre dos dientes consecutivos del piñón. Esta ecuación es válida para un sistema sin falla. Para una falla en el diente 1 de la corona, la ecuación 5 resulta:

(6) Tp_falla = Fp_fallaRp [0 + cos (α) + cos (α + βp)]

Luego, haciendo el cociente entre la ecuación 6 y la 5, y reemplazando la relación entre Fp_falla/Fp dada por la ecuación 4 se obtiene el valor que tendrá el par resistente visto desde el lado del piñón cada vez que el diente defectuoso se halla en la posición dada por d1 en la figura 1. Se considera que el tiempo en que un diente ocupa cada una de las posiciones indicadas en la figura 1 es igual al tiempo de rotación de la rueda dividido el número de dientes.

(7) Tp_falla/Tp = [cos(α + βp) + cos (α) + cos (α − βp)] / [cos (α) + cos (α − βp)]

La ecuación 7 permite calcular la perturbación en el par medio transmitido por el piñón cada vez que el diente defectuoso se halla ocupando la posición d1. De manera similar es posible aplicar las ecuaciones 2 a 7 a las posiciones d2 y d3 para el diente defectuoso.
El paso completo del diente defectuoso por la zona de engrane define una perturbación como le presentada en la figura 2. Tal como se observa, inicialmente el par resistente que se presenta sobre el piñón resulta levemente disminuido, luego, se observa un sobrepar.

3. Modelo del motor de inducción y estimador de par

Con el fin de simular el funcionamiento del motor de inducción en régimen transitorio se emplea el conocido modelo basado en la transformación de Park. Este modelo se basa en el tratamiento de las variables eléctricas del motor sobre un sistema de ejes en cuadratura, generalmente denominados “ejes ficticios”, e indicados por las letras “d” y “q”. El desarrollo de este modelo deriva en las ecuaciones 8 a 15.

(8) vds = pλds − λqs pθr + Rs ids
(9) vqs = pλqs − λds pθr + Rs iqs
(10) v’dr = pλ’dr + R’r i’dr
(11) v’qr = pλ’qr − λqs + R’r i’qr
(12) λds = Ls ids + M (ids + i’dr)
(13) λqs = Ls iqs + M (iqs + i’qr)
(14) λ’dr = L’r i’dr + M (ids + i’dr)
(15) λ’qr = L’r i’qs + M (iqs + i’qr)

En las ecuaciones 8 a 15, p representa al operador (d/dt), λ a los enlaces de flujo magnético, i a las corrientes, v a los voltajes, Rs es la resistencia por fase del estator y R’r la del rotor referida al estator. Asimismo, Ls y L’r son las inductancias de dispersión del estator y del rotor referida al estator, M es la inductancia mutua máxima entre bobinas del estator y bobinas del rotor, θr indica la posición del rotor respecto al marco de referencia fijo al estator y ω r la velocidad angular del rotor. Los subíndices d y q hacen referencia al sistema de ejes ficticios obtenidos a partir de la transformación de Park.
Las ecuaciones anteriores se completan con las siguientes expresiones de par eléctrico producido por el motor y par de carga:

(16) Te = (3/2) (P/2) (λds iqs − λqs ids)
(17) Te = Jpω r + T_carga

donde J es la inercia rotacional del conjunto rotor-carga en [kgm²], P el número de polos y T_carga el par de la carga en Nm. Teniendo en cuenta que una de las técnicas para detectar fallas que será evaluada en este trabajo consiste en el análisis del par eléctrico, y que dicha variable solo puede deducirse a partir de la medición de variables externas (tensiones y corrientes) se propone a continuación un modelo para efectuar dicha estimación. En el sistema de ejes en cuadratura, el par eléctrico está dado por la ecuación 16.
Los enlaces de flujo, por su parte, pueden obtenerse a partir de los voltajes y corrientes de estator:
(18) λs (t) = ₀∫¹ [Vs (t) - Rs . Is ] . dt + λs

donde los voltajes y corrientes se indican en forma de vectores espaciales y están dados por:

(19) vs(t) = vds(t) + j vqs(t)
(20) is(t) = ids (t) + j iqs(t)

De este modo, sensando las corrientes de estator y los voltajes aplicados al motor y conociendo el valor de la resistencia de estator, es posible estimar el par eléctrico del motor.

Figura 3. Sistema con dos etapas reductoras.

4. Ejemplo de aplicación

El modelo presentado se utilizará para analizar una situación de falla en el reductor de velocidad esquematizado en la figura 3. Las simulaciones se efectúan en Matlab®/Simulink. El motor que acciona al reductor de velocidad es un motor de inducción trifásico de 1,5 kW, 380 V, cuatro polos, alimentado desde la red eléctrica. Las características del motor se obtuvieron de Chee-Mun Ong (1998). El reductor, por su parte, consta de dos etapas reductoras, las características de cada una de las ruedas dentadas se presentan en la tabla 1. La falla a simular consiste en la rotura en un diente de la corona 2. La velocidad de rotación de esta rueda es de 11,2 revoluciones por segundo. Esto significa que el diente defectuoso pasará por la zona de engrane 11,2 veces por segundo, de ahí que dicha frecuencia se defina como la frecuencia de falla. Por consiguiente, la falla debería provocar un armónico a la frecuencia de falla y sus múltiplos en el par eléctrico.
Sobre la corriente, la falla debería manifestarse a frecuencias dadas por:

(21) fIs = f ± k f_falla

donde fIs son las frecuencias en la corriente de estator que denotan falla, f es la frecuencia de red, en este caso 50 Hz, ffalla es la frecuencia de rotación de la rueda con falla y k representa a los números enteros.

Figura 4. Comparación entre el par de la corona (rojo) y el par electromagnético del motor (azul).

A partir de las ecuaciones 4 y 7, se calculan las perturbaciones que sufre el par observado por el piñón cada vez que pasa por la zona de engrane el diente defectuoso. En la figura 4 se presenta la variación temporal del par que el piñon debe realizar sobre la corona. Las perturbaciones resultan a una frecuencia dada por la frecuencia de falla y, dado que el conjunto piñón-corona tiene en este caso tres dientes en contacto simultáneamente, la perturbación consta de tres etapas, cada una de la cuales tienen una duración igual al tiempo que tarda la corona en girar un paso de diente, esto es, el tiempo que tarda la corona en dar una vuelta dividido el número de dientes. El par electromagnético del motor, por su parte, no puede seguir fielmente estos incrementos de par resistente dado que la inercia rotacional impide cambios bruscos en su valor. Tal como se muestra en la figura 4, en azul, las variaciones en el par eléctrico son de menor amplitud y dependen del valor de inercia total asociada al sistema compuesto por el motor, el reductor y la carga. Las gráficas presentadas en la figura 4 fueron obtenidas con una inercia total igual a dos veces la inercia propia del motor.
El valor de βc se obtiene de la ecuación 1, mientras que βp se calcula adaptando la ecuación 1 a las características del piñón tal como se expresa en la ecuación 23:

(22) βc = 360° / Zc = 360° / 55 = 6,54°
(23) βp = 360° / Zp = 360° / 35 = 10,29°

Figura 5. Espectro de frecuencia del par electromagnetic estimado expresado en dB.

En la figura 5 se presenta el espectro de frecuencias del par estimado para la condición de falla. El caso presentado corresponde a una carga sobre el motor igual a la mitad de su capacidad nominal y con una inercia total igual a dos veces la inercia propia del rotor. Se observa claramente las componentes a la frecuencia de falla y sus múltiplos. El valor de la amplitud de la componente a 11,3 Hz resulta de aproximadamente 140 dB. Esta frecuencia se vería levemente modificada para otros estados de carga del motor debido al deslizamiento.

De la figura 5 es posible deducir que la falla queda perfectamente señalada en el espectro de frecuencia del par eléctrico.

5. Conclusiones

El modelo desarrollado con el fin de representar el comportamiento de un accionamiento con una falla en uno de los dientes de la caja reductora ha sido probado mediante simulaciones. Los resultados obtenidos, en cuanto a frecuencias de falla, coinciden con los presentados por otros autores. El modelo propuesto presenta la posibilidad de una rápida adaptación a otras combinaciones de ruedas.
Se espera proximamente contar con un banco de ensayos que permita validar experimentalmente las conclusiones anteriores. Se estudiará, además, en futuros trabajos, la posibilidad de separar fallas en engranajes de otro tipo de fallas que podrían presentar frecuencias de falla coincidentes (por ejemplo, desbalance de masas) y fallas más severas en engranajes (deterioro de dos dientes, ya sean consecutivos o no).

Nota del editor: el estudio aquí presentado se asienta sobre una extensa bibliografía que por razones editoriales elegimos no publicar. Para consultas de este tipo, contactar a los autores.
Nota del editor: Este trabajo fue originalmente presentado por los autores en el congreso y exposición AADECA 2014, celebrado durante octubre de 2014 en diversas sedes de la ciudad de Buenos Aires, organizado por AADEC

Contacto: Ing. Carlos Verucchi