La diferencia esencial entre las corrientes eléctricas alternas a 50 o 60 Hz y las corrientes impulsivas i = f (t, Imáx.; t1; t2) es que las corrientes impulsivas pueden ionizar el suelo cuando se dispersan mediante uno o más electrodos (jabalinas, mallas, etc.) durante la conducción a tierra de la corriente de los rayos.
Las corrientes alternas calientan el suelo pero las corrientes impulsivas calientan, ionizan y pueden perforar/atravesar esa interfaz electrodo-suelo y algunas capas (estratos) del terreno y evaporar el agua de la humedad del suelo circundante a los electrodos de puesta a tierra.
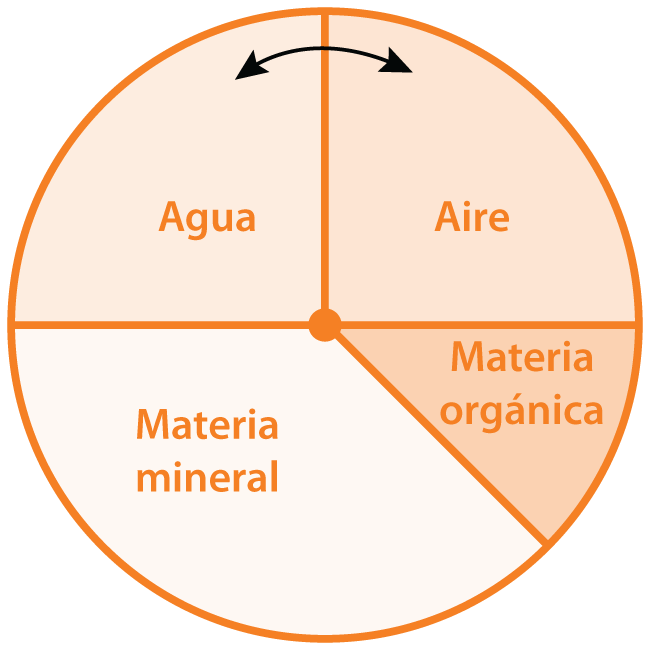
La corriente impulsiva i = f (t, Imáx.; T1; T2), cuando pasa de un electrodo metálico hacia el suelo donde está enterrado, produce un campo eléctrico (gradiente de potencial) que puede ionizar este suelo circundante haciéndolo más electroconductor durante el tiempo que dure la ionización de los cuatro componentes del suelo: aire, agua, materia mineral, materia orgánica (ver figura 1).
| Investigador | Año | Campo eléctrico crítico de ionización del suelo (valores límites) | Referencia bibliográfica |
|---|---|---|---|
| H. M. Towne | 1929 | 160 a 520 kVc/m | [1] |
| P. L. Bellaschi | 1941 | 120 a 420 kVc/m | [2] [3] |
| A. C. Liew, M. Darveniza | 1974 | 300 kVc/m | [4] |
| M. Loboda; Z. Pochanke | 1985 | 560 a 900 kVc/m | [5] |
| E. E. Oettle | 1988 | 600 a 1850 kVc/m (600 a 800 suelos muy húmedos) | [7] |
| CIGRE | 1991 | 400 kVc/m | [8] |
| A. M. Mousa | 1994 | 300 kVc/m | [9] |
| I. F. Gonos et alles | 2004 | 200 kVc/m | [10] |
| N. M. Nor et alles | 2006 | 550 kVc/m para celda hemiesférica, 790 para placas paralelas | [11] |
Tabla 1. Valores del campo eléctrico crítico (Ec) de ionización de suelos según varios investigadores desde 1929 a 2007 [19].
| Tipo de suelo | Campo eléctrico (gradiente) de ionuzación del suelo (Ec). Valores límites probables | Resistividades volumétricas estimadas. Valores típicos y límites normales |
|---|---|---|
| Arcilla plástica (húmeda) | 1870-3900 kVc/m | 50 (8 a 70) Ωm |
| Arena seca | 1710-1880 kVc/m | 5000 (3000 a 8000) Ωm |
| Arena húmeda | 1300-2340 kVc/m | 800 (200 a 3000) Ωm |
| Grava seca | 2080-2280 kVc/m | 15.000 (3000 a 30.000) Ωm |
| Grava húmeda | 1140-1920 kVc/m | 3000 (40 a 10.000) Ωm |
Tabla 2. Valores límites probables del campo eléctrico de ionización del suelo según los tipos de suelos y sus resistividades volumétricas estimadas [21] [22].
En la figura 1 se ilustra una representación esquemática simplificada de un suelo de textura media. Según Cabrera, el 50% del volumen es materia sólida, que es mineral y orgánica. Dentro del otro 50% se encuentra agua y aire en proporciones del 25% cada uno, que están presentes dentro de los espacios vacíos dejados por los granos del suelo. La flecha en la parte superior de la figura indica la variación que se puede presentar entre los contenidos del agua y del aire, indicando que el incremento de una cantidad está asociado con el decrecimiento de la otra.
En la figura 2 se muestran unas curvas típicas del comportamiento del suelo ante impulsos de rayos y se destaca el comportamiento de la resistencia que presenta varios estados de disminución y de recuperación de la resistencia en el tiempo.
La mayoría de los suelos consisten en numerosas partículas con un cierto grado de humedad y también puede haber una cantidad de sales disueltas. El aire también forma parte de esa composición física que llena los espacios vacíos disponibles en el conjunto de partículas que forman la composición del suelo. Es decir que el suelo está conformado principalmente por granos, agua y aire, que son los que regulan el proceso de inicio y desarrollo de la descarga eléctrica en el interior del suelo. El agua cumple un papel fundamental en la conductividad eléctrica del suelo y de cuya cantidad depende la buena conducción eléctrica del suelo junto con la cantidad de sal disuelta en dicha agua. La cantidad de aire está determinada por los volúmenes de espacio disponible dejado por los granos y cantidad de agua contenida en la arena. El aire contenido en esta arena es parte importante del estudio en los trabajos de investigación ([19] y [20]).
Los suelos con granos de gran tamaño (grava) tienen espacios de aire mayores comparados con aquellos suelos donde los granos son del orden de los milímetros. Entonces los espacios de aire contenidos son también espacios no homogéneos, sin un tamaño predefinido y sin geometrías regulares. La configuración de electrodos utilizada también determina el comportamiento de estos tres elementos (agua, granos, aire) dentro de una muestra de suelo. Es el caso de la configuración de electrodos coaxiales utilizada en estas investigaciones.
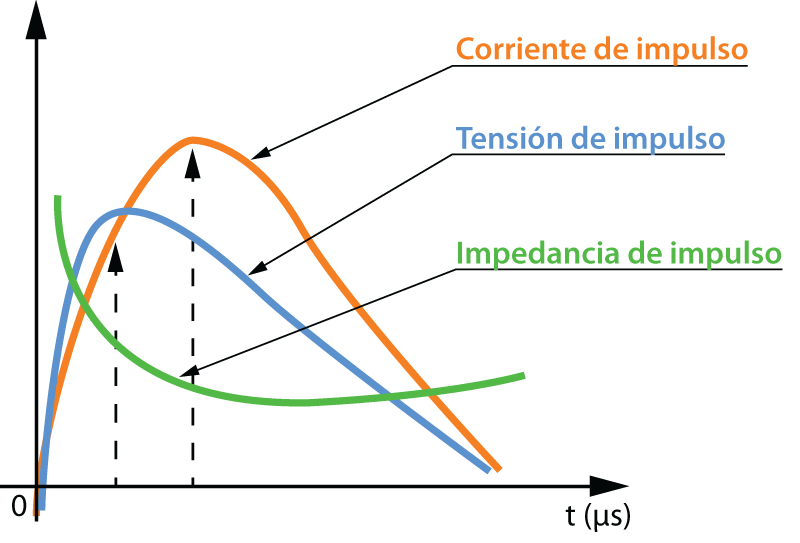 Figura 2. Curvas típicas para la tensión, la corriente y la impedancia del fenómeno de descarga eléctrica impulsiva en suelos.
Figura 2. Curvas típicas para la tensión, la corriente y la impedancia del fenómeno de descarga eléctrica impulsiva en suelos.Medidas de los electrodos de la figura 4 según [19] y [20]:
- L (largo): 60 y 70 cm
- a (radio de electrodo interno): 0,5 y 0,48 cm
- b (radio de electrodo externo): 7,3 y 12,7 cm
[1] Ec = a.ρb
que da el valor del campo eléctrico como Ec (kVc/m) de ionización de las muestras de suelos alrededor del electrodo central de radio “a”, cuando se aplican las tensiones impulsivas Ua = f (t, Umáx.; T1; T2) contra la tierra conectada al electrodo exterior. El campo eléctrico de ionización de cada uno de los suelos tiene su valor crítico Ec (kVc/m), que es el valor que tiene el campo eléctrico cuando comienza la ionización que ocurre en el suelo después de la conducción electrolítica en la interfaz electrodo-suelo, que es la que inicia la ionización según el ilustre Karl Berger [22].
La conducción electrolítica ocurre solamente cuando es baja la densidad de corriente que fluye desde la superficie electródica metálica hacia la tierra adyacente. Así, la intensidad del campo eléctrico Ea, en la interfaz electrodo-suelo Ea = ρ.Ja no supera los 2 kVc/cm = 200 kVc/m
Cuando la corriente aumenta, se produce calor en la interfaz electrodo-suelo y aumenta la temperatura del suelo contiguo a la interfaz (por efecto Joule). De esta manera, se evapora el agua que humedecía el suelo circundante al electrodo y simultáneamente aumentan la resistividad superficial y la intensidad del campo eléctrico Ea = ρ.Ja con gran velocidad.
En la interfaz electrodo-suelo circundante, se crea una zona de descargas: primero en forma de canales de chispas paralelos entre sí, y después, en la forma de canales de arcos eléctricos precedidos de los canales de chispas, a medida que aumenta la intensidad del campo electrocinético Ea que adquiere un valor crítico Ec.
Es posible que la zona de canales (de chispas y de arcos) cause un aumento aparente en las dimensiones (principalmente el diámetro) del electrodo dispersor con lo que resulta una disminución de la resistencia de dispersión hasta llegar a un mínimo que es la Rmín. (Ω) (figuras 4 y 5).
Esta disminución de la resistencia se debe a que la caída de tensión en la zona de canales es mucho menor que la que hay en el caso de conducción electrolítica.
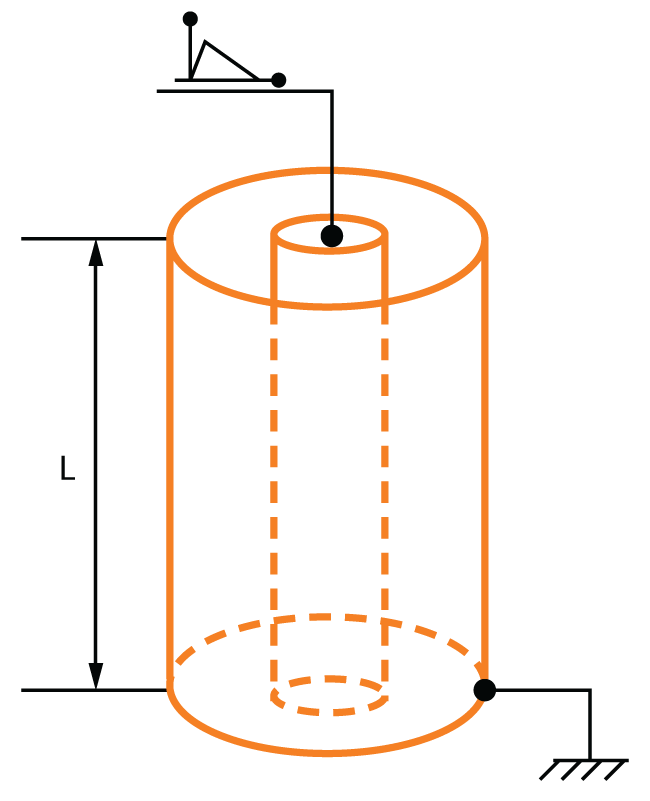
Los canales de chispas y de arcos son rápidamente enfriados por el suelo circundante, y a medida que los canales se alargan, aumenta también la caída de tensión a lo largo de ellos. Esto limita el radio a* de alcance de la zona de canales (figura 4).
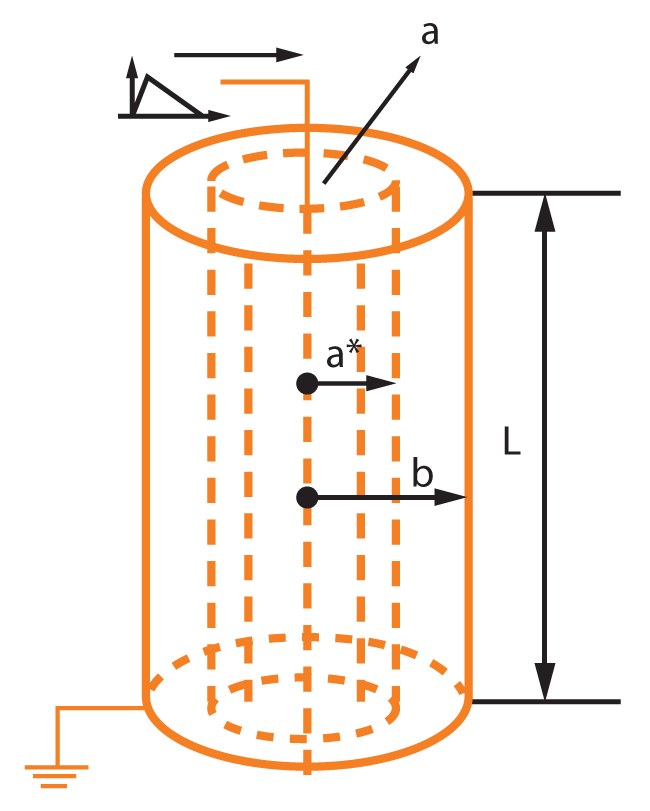 Figura 4. Configuración del modelo de Pedro Pineda.
Figura 4. Configuración del modelo de Pedro Pineda.Dimensiones de los electrodos: a: radio del electrodo interno
a*: radio de la zona ionizada | b: radio del electrodo externo
L: largo de los electrodos
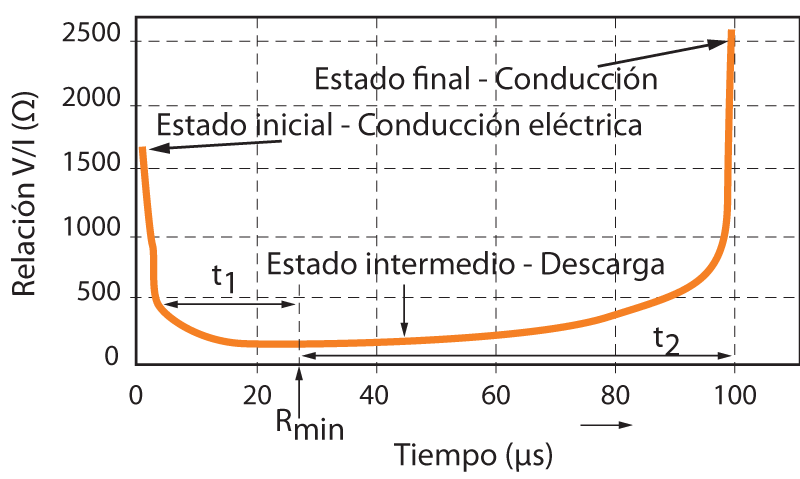 Figura 5. Curva experimental (V/I) = f (t)
Figura 5. Curva experimental (V/I) = f (t)t1: tiempo hasta alcanzar la Rmín de la curva (V/I) en la descarga.
t2: tiempo hasta llegar al estado final de la descarga impulsiva y que el suelo recupere la conducción de la corriente eléctrica
| Línea de la figura | Figura (nomograma bilog) | Coeficiente a de la ecuación (1) | Exponente b de la ecuación (1) | Autores | Referencia bibliográfica |
|---|---|---|---|---|---|
| A | 6 (A, B) | 241 | 0,215 | Oettle | [7] |
| B | 6 (A, B) | 1986 | 0,124 | Manna | [15], [17] |
| C | 7 (A, B, C, D) | 75 | 0,476 | Nor | [13], [18] |
| D | 7 (A, B, C, D) | 62,4 | 0,52 | Loboda | [6] |
| E | 8 (A, B, E) | 68 | 0,5 | Arcioni | Media geométrica C y D en esta nota |
| F | 9 (A, B, E, F) | 59,8 | 0,61 | Rincón Ávila | [20] |
Tabla 3. Cuadro de resumen de las ecuaciones del campo eléctrico crítico Ec (kVc/m) de ionización de los suelos de resistividad volumétrica ρ (Ωm)
Nota: en la función monómica Ec = a.ρb, el coeficiente “a” tiene la unidad kVc/m como el campo Ec, pero el exponente “b” es adimensional y la resistividad tiene la medida (número) del parámetro ρ (Ωm)
| ρ (Ωm) | Emg (kVc/m) |
|---|---|
| 10 | 373 |
| 100 | 958 |
| 1000 | 2462 |
| 2000 | 3272 |
| 4000 | 4347 |
Tabla 4. Algunos valores de la función G.
En la (G) tenemos: b = 1/6 Σ (bi) y Amg = [Π (ai)]1/6. Hacemos los cálculos y así resultan estos valores:
- Amg ≈ 145 kv/m
- b ≈ 0,41
En la figura 10 representamos a la función G juntamente con A y B. Se puede apreciar que la función G para el intervalo de valores (11 ≤ ρ ≤ 8000) está entre las funciones A y B. Es decir que para ρ ≈ 11 Ωm, A y G se cortan en un punto, y para ρ ≈ 8000 Ωm, B y G se cortan en otro punto distinto.
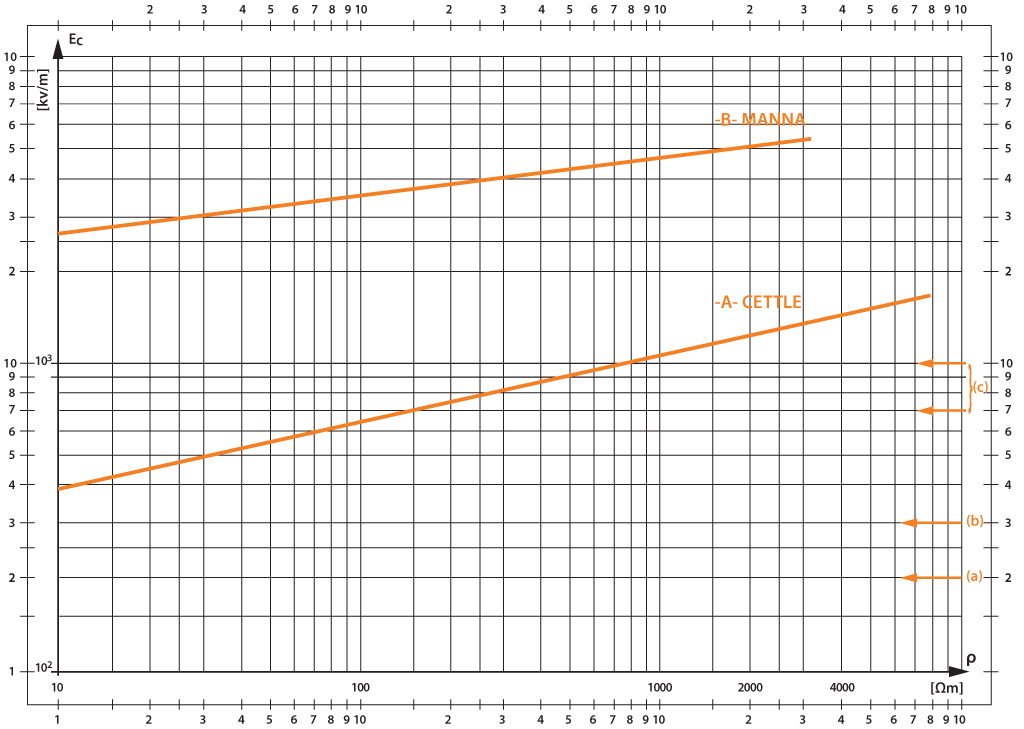 Figura 6. Nomograma bilogarítmico de la función Ec (kVc/m) = a.ρb del campo eléctrico crítico de ionización del suelo alrededor de un electrodo de puesta a tierra en función de la resistividad volumétrica ρ (Ωm). Autor: Oettle (A). Manna (B)
Figura 6. Nomograma bilogarítmico de la función Ec (kVc/m) = a.ρb del campo eléctrico crítico de ionización del suelo alrededor de un electrodo de puesta a tierra en función de la resistividad volumétrica ρ (Ωm). Autor: Oettle (A). Manna (B)Línea: A, B | Valores: a, 241 y 1986 kVc/m; b, adimensional 0,215 y 0,124, y ρ, valor numérico (medida) de Ωm
Notas: en el gráfico bilogarítmico se marcan a la derecha los valores siguientes:
a: Emce = 200 kVc/m = valor máximo para la conducción electrolítica (Kostaluk, Loboda et al.)
b: Edep = 300 kVc/m = valor mínimo para producir descargas en poros o entre partículas del suelo (Berger)
c: Epc = 700 a 1000 kVc/m = valores para producir descargas entre capas del suelo (Berger)
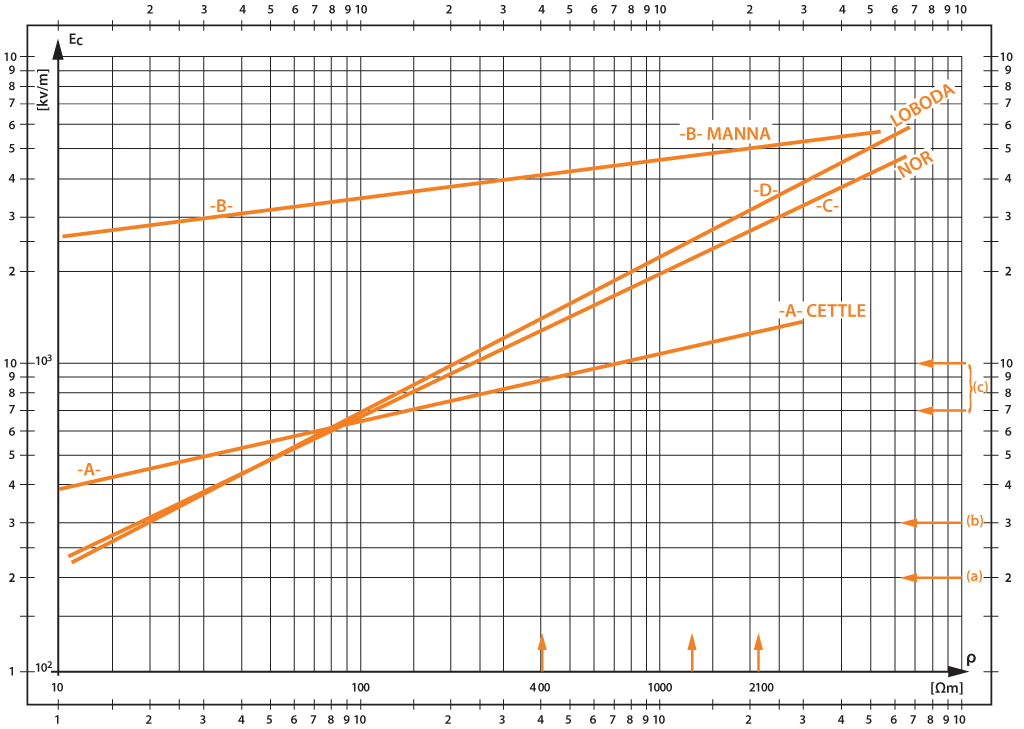 Figura 7. Nomograma bilogarítmico de la función Ec (kVc/m) = a.ρb del campo eléctrico crítico de ionización del suelo alrededor de un electrodo de puesta a tierra en función de la resistividad volumétrica ρ (Ωm). Autores: Oettle, Manna, Nor, Loboda
Figura 7. Nomograma bilogarítmico de la función Ec (kVc/m) = a.ρb del campo eléctrico crítico de ionización del suelo alrededor de un electrodo de puesta a tierra en función de la resistividad volumétrica ρ (Ωm). Autores: Oettle, Manna, Nor, LobodaLínea: A, B C, D | Valores: a, 241 y 1986 kVc/m; b, adimensional 0,215, 0,124, 0,476 y 0,520, y ρ, valor numérico (medida) de Ωm
Notas: en el gráfico bilogarítmico se marcan a la derecha los valores siguientes:
a: Emce = 200 kVc/m = valor máximo para la conducción electrolítica (Kostaluk, Loboda et al.)
b: Edep = 300 kVc/m = valor mínimo para producir descargas en poros o entre partículas del suelo (Berger).
c: Epc = 700 a 1000 kVc/m = valores para producir descargas entre capas del suelo (Berger).
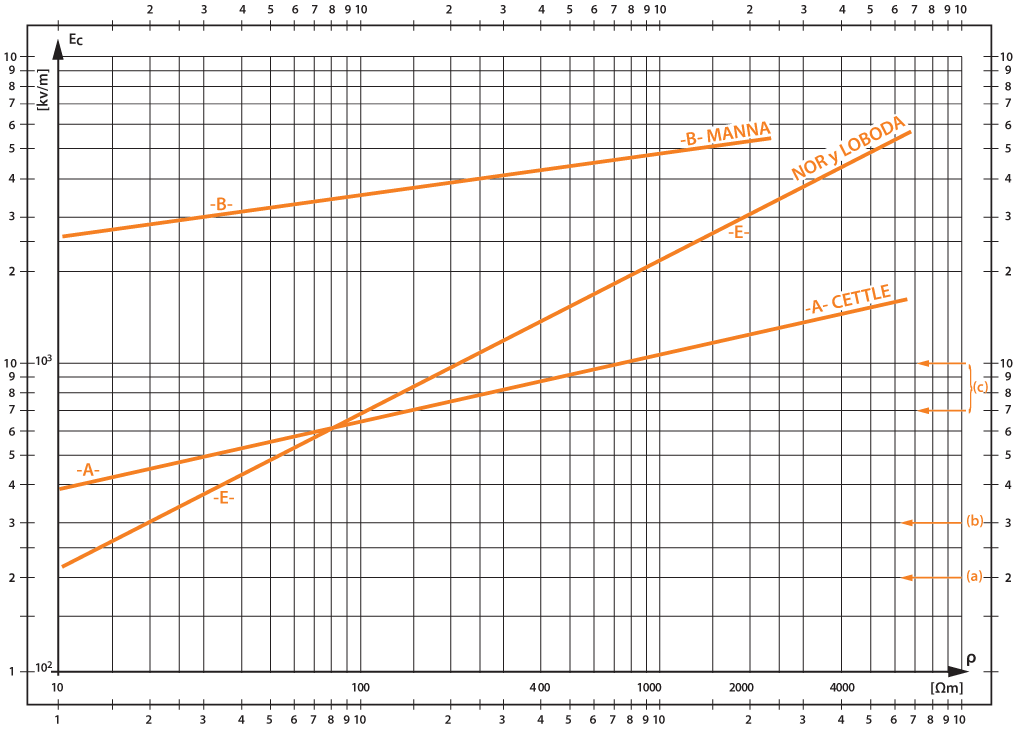 Figura 8. Nomograma bilogarítmico de la función Ec (kVc/m) = a.ρb del campo eléctrico crítico de ionización Ec del suelo alrededor de un electrodo de puesta a tierra en función de la resistividad volumétrica ρ (Ωm). Autores: Oettle, Manna, Nor, Loboda
Figura 8. Nomograma bilogarítmico de la función Ec (kVc/m) = a.ρb del campo eléctrico crítico de ionización Ec del suelo alrededor de un electrodo de puesta a tierra en función de la resistividad volumétrica ρ (Ωm). Autores: Oettle, Manna, Nor, LobodaLínea: A, B, E | Valores: a, 241, 1986 y 68 kVc/m; b, adimensional 0,215, 0,214 y 0,5, y ρ, valor numérico (medida) de Ωm
Notas: en el gráfico bilogarítmico se marcan a la derecha los valores siguientes:
a: Emce = 200 kVc/m = valor máximo para la conducción electrolítica (Kostaluk, Loboda et al.)
b: Edep = 300 kVc/m = valor mínimo para producir descargas en poros o entre partículas del suelo (Berger).
c: Epc = 700 a 1000 kVc/m = valores para producir descargas entre capas del suelo (Berger).
 Figura 9. Nomograma bilogarítmico de la función Ec (kVc/m) = a.ρb del campo eléctrico crítico de ionización Ec del suelo alrededor de un electrodo de puesta a tierra en función de la resistividad volumétrica ρ (Ωm). Autores: Oettle, Manna, Nor, Loboda, Rincón Ávila
Figura 9. Nomograma bilogarítmico de la función Ec (kVc/m) = a.ρb del campo eléctrico crítico de ionización Ec del suelo alrededor de un electrodo de puesta a tierra en función de la resistividad volumétrica ρ (Ωm). Autores: Oettle, Manna, Nor, Loboda, Rincón ÁvilaLínea: A, B, E, F | Valores: a, 241, 1986, 68 y 59,8 kVc/m; b, adimensional 0,215 y 0,124, y ρ, valor numérico (medida) de Ωm.
Notas: en el gráfico bilogarítmico se marcan a la derecha los valores siguientes:
a: Emce = 200 kVc/m = valor máximo para la conducción electrolítica (Kostaluk, Loboda et al.)
b: Edep = 300 kVc/m = valor mínimo para producir descargas en poros o entre partículas del suelo (Berger)
c: Epc = 700 a 1000 kVc/m = valores para producir descargas entre capas del suelo (Berger)
[1] Towne, “Impulse characteristics of driven grounds”, Gen. Electr. Rev. pp. 605-609, Nov. 1929
[2] Bellaschi, “Impulse and 60-cycle characteristics of driven grounds”, Transactions Am. Inst. Electr. Eng., vol. 60, pp. 123-128, Mar. 1941
[3] Bellaschi; Armington; Snowden, “Impulse and 60-cycle characteristics of driven grounds II”, Transactions Am. Inst. Electr. Eng., vol. 61, pp. 349-363, 1942
[4] Liew; Darveniza, “Dynamic model of impulse characteristics of concentrated earths”, en Proc. IEE, vol. 121, núm. 2, pp. 123-135, Feb. 1974
[5] Loboda; Pochanke, “Experimental study of electric properties of soil with impulse current injections” en Proc. of 18° International Conference of Lightning Protection, pp. 191-198, Múnich, 1985
[6] Loboda; Scuka, “On the transient characteristics of electrical discharges and ionization processes in soil”, en Proc. of 23° International Conference on Lightning Protection, pp. 539-544, 1966
[7] Oettle, “A new general estimation curve for predicting the impulse impedance of concentrated Earth electrodes”, en IEEE Transactions on Power Delivery, vol. 3, núm. 4, pp. 2020-2029. 1988
[8] CIGRE Working Group on Lightning, Guide to procedures for estimating the lightning performance of transmission lines, CIGRE, 1991
[9] Mousa, “The soil ionization gradient associated with discharge of high currents into concentrated electrodes”, en IEEE Transactions on Power Delivery, vol. 9, núm. 3, pp. 1669-1677, 1994
[10] Gonos; Stathopulos, “Soil ionization under lightning impulse voltages”, IET Proceedings Science, Measurement and Technology, vol. 151, núm. 5, pp. 343-346, Sept. 2004
[11] Nor; Haddad; Griffiths, “Characterization of ionization phenomena in soils under fast impulses”, en IEEE Transactions on Power Delivery, vol. 21, núm. 1, pp. 353-361, Ene. 2006
[12] Nor; Haddad; Griffiths, “Performance on earthing systems of low resistivity soils”, en IEEE Transactions on Power Delivery, vol. 21, núm. 4, pp. 2039-2047, Oct. 2006
[13] Nor; Ramli, “Electrical properties of dry soil under high impulse currents”, en Journal of Electrostatics 65, pp. 500-505, Elsevier, 2007
[14] Lima; Visacro, “Experimental developments on soil ionization” en Proc. of International Conference on Grounding and Earthing y 3° International Conference on Lightning Physics and Effects, pp. 174-179, Brasil
[15] Manna; Chowdhuri, “Generalized equation of soil critical electric field Ec based on impulse tests and measured soil electrical parameters”, IET Generation Transmission and Distribution, vol I, núm. 5, pp. 811-817, 2007
[16] IEC-60-1, Guide on high voltage testing techniques. Standards, 1989
[17] Manna, “Impulse impedance of grounding systems and its effects on tower crossarm voltage”, dissertation, Ago. 2006
[18] Nor; Ramli, “Effects of moisture content, impulse polarity and earth electrode’s dimension on dry and wet sand under high voltage conditions”, ETEP Transactions on Electrical Power, vol. 18, pp. 461-475, Jun. 2007
[19] Asimakopoulou; Gonos; Stathopulos, Experimental investigation on soil ionization, NTUA, Atenas
[20] Rincón Ávila, Edisson Javier, Estudio termo-eléctrico de la disrupción eléctrica en arena bajo impulsos tipo rayo, Universidad de Colombia, Bogotá, 2010
[21] Kindermann, Geraldo; Campagnolo, Jorge Mario, Aterramento elétrico, Sagra-DC Luzzatto Editores, RS, Brasil, 1992
[22] Arcioni, Juan Carlos, Puesta a tierra de instalaciones y sistemas eléctricos de BT, MT y AT, Universitas, Córdoba, 2006