Presentamos una recapitulación de conceptos sobre la física básica de los rayos, y definimos la distancia de cebado (también llamada “distancia disruptiva” o “de impacto” o “de atracción de rayos”) por una punta o una estructura puesta a tierra. Comentamos varias expresiones matemáticas de estas distancias y su relación con los radios de la esfera rodante.
1. Los radios de la esfera rodante del método electrogeométrico para diseñar las protecciones contra rayos y las distancias de atracción de los rayos en los pararrayos
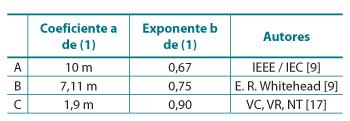
Tabla 1. Distancias disruptivas Ds según distintos autores, siendo Ds = a . Ipb
1.1 En el “Anexo A”, recapitulamos los conceptos de la física básica de los rayos, la actuación de los pararrayos y los modelos matemáticos del impacto de los rayos [13].
1.2 En el apartado A.4 del Anexo A, definimos la distancia disruptiva –DS-, también llamada “distancia de cebado” (de un arco eléctrico) -ver figura A2-. La distancia Ds es una función de la corriente presunta Ip del trazador positivo ascendente del retorno de las cargas positivas de la tierra a la nube que fueron inducidas en la tierra por el trazador descendente nube-tierra, que desplaza las cargas negativas de la nube a la tierra.
La distancia disruptiva o de cebado Ds es una función de la corriente presunta Îp, que se expresa con la fórmula (1).
(1) Ds = a . Îpb
Siendo:
Ds (m), la distancia disruptiva o de cebado.
a (m), un coeficiente empírico.
Îp (kAc), la corriente presunta (valor de cresta).
b (adimensional), un exponente empírico
En la figura 1, representamos la fórmula 1 en las líneas A, B y C.
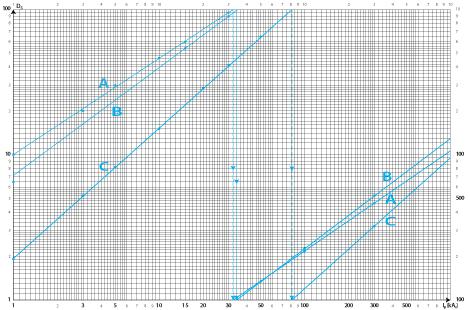 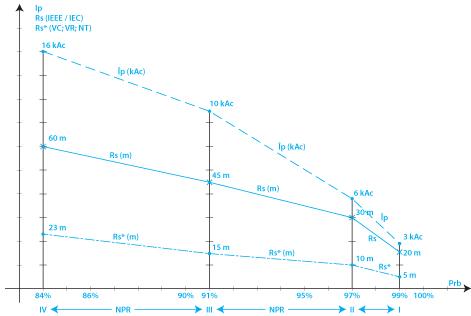 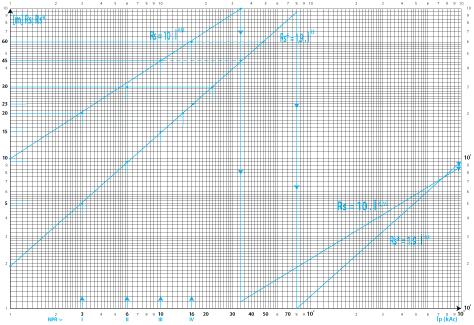
Figura 1. Distancias disruptivas Ds = a (Ip)b en líneas A, B y C de la tabla 1.
Figura 2.1.a. PCR (protección contra rayos). MDLER (métodos de la esfera rodante). Comparación equiprobabilística entre los radios de la esfera rodante Rs y Rs* en función de la misma corriente presunta Îp de la descarga de retorno tierra-nube (para los rayos negativos descendentes nube-tierra según las IEEE/IEC) y los autores Cooray, Rakov y Theetayi [17].
Figura 2.1.b. Comparación equiprobabilística entre Rs y Rs* para Ip = Ip*.
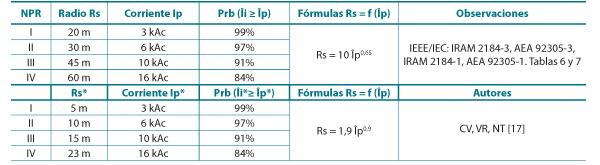
Tabla 2.1 de radios Rs máximos y mínimos en función de la Ip y sus probabilidades Prb (Îi ≥ Îp) asociadas y niveles de protección (NPR)
2. Los radios de la esfera rodante Rs para las distancias Ds = a . Îpb y las corrientes presuntas Ip de retorno
El radio Rs de la esfera rodante (o ficticia) del modelo electrogeométrico [9] se define que es igual a la distancia disruptiva o de cebado Ds.
Tenemos entonces la igualdad siguiente:
(2) Rs = Ds = f (Îp) = a Îpb
A continuación, estudiamos los radios Rs = 10 Îp0,67 y Rs* = 1,9 Îp0,9 de la tabla 1.

Figura 2.2. Comparación entre las corrientes Îp, Îp* e Îpmg para los radios Rs = Rs* de la esfera rodante según las IEEE/IEC y los autores Cooray, Rakov y Theetayi [17].
Nota: corrientes presuntas de las descargas de retorno a la nube de las cargas positivas (tierra-nube) (para los rayos negativos descendentes nube-tierra):
• Ip es la corriente según IEEE/IEC.
•Ip* es la corriente según Cooray, Rakov y Theetayi [17].
• Ipmg es la corriente media geométrica entre Îp e Îp*.
Caso 2.1. Comparación entre los radios Rs y Rs* para Îp = Îp*, que es la comparación equiprobabilística de la tabla 2.1 y las figuras 2.1.a en coordenadas lineales y 2.1.b en coordenadas bilogarítmicas.
Conclusiones: los radios Rs son casi tres veces mayores que los Rs* para las mismas corrientes Îp = Îp* de las normas IEC e IRAM-AEA.
Caso 2.2. Comparación entre los radios iguales Rs = Rs* para las respectivas corrientes Îp e Îp* de probabilidades Prb (Îi ≥ Îp) y Prb (Îi* ≥ Îp*) [19].
En la tabla 2.2, tenemos la comparación entre Ip e Ip* para Rs = Rs*. Notamos que Ip* > Ip para Rs = Rs* en los NPR I, II, III y IV (niveles de protección contra rayos normalizados por IEC e IRAM-AEA) de la figura 2.2.
Entre las corrientes Ip e Ip* para cada Rs = Rs* calculamos la corriente media-geométrica: Ipmg = √(Ip . Ip*), cuya expresión para el radio Rs es Rs ≈ 4,8 (Îpmg)0,76.
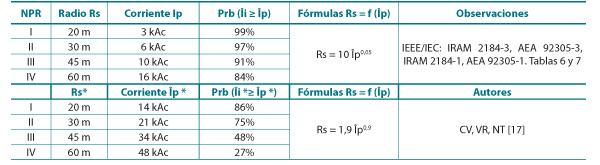
Tabla 2.2. Comparación entre los radios Rs = Rs* de la esfera rodante en función de las respectivas corrientes presuntas Îp e Îp* de las descargas de retorno tierra–nube (para los rayos negativos descendentes nube-tierra) según las IEEE/IEC y los autores Cooray, Rakov y Theetayi [17]. Tabla de radios Rs = Rs* en función de Îp e Îp* y sus probabilidades Prb (Îi ≥ Îp) asociadas y niveles de protección (NPR).
3. Conclusiones generales y propuesta de los autores
3.1 En la tabla 3, comparamos las tres corrientes Îp, Îp* e Îpmg con sus probabilidades Prb (Îi ≥ Îp) respectivas, para iguales radios normalizados de 20, 30, 45 y 60 m, que son Rs = Rs*, que quedan sin cambios por hipótesis.
La expresión (2) da corrientes Ip*, que son unas cinco a tres veces mayores que las Îp de la (1) para Rs = Rs*. Y sus probabilidades son entre el 13 y el 68% menores que las corrientes Îp.
3.2 Por esta razón, los autores calcularon una propuesta intermedia entre Ip e Ip*: mediante las medias geométricas Ipmg, siendo Îpmg = √ (Ip . Ip*) que están entre los valores Îp e Îp* con probabilidades intermedias que se indican en la tabla 3. Pero todas las Prb (Îi ≥ Îp) son mayores que el 50% y se mantienen sin cambios los radios normalizados Rs = (20, 30, 45, 60 m), como los autores estimaron que ocurriría en la IEC.

Tabla 3. Comparación de corrientes y sus probabilidades Prb (Îi ≥ Îp) para Rs = Rs*.
Anexo A. Reseña de la física de los rayos, la actuación de los pararrayos y los modelos matemáticos del impacto de los rayos.
A1. Actuación de los pararrayos, distancia de cebado o disruptiva, efectividad de las protecciones contra rayos [13].
A1.1. El impacto de un rayo en un pararrayos franklin ocurre mediante un trazador conector (conecting leader) que sale de la punta del pararrayos dirigida hacia el trazador descendiente por pasos que está en el extremo del rayo nube–tierra (downcorning stepped leader).
A1.2. La salida exitosa del trazador conector desde el pararrayos hacia el rayo descendente requiere la formación de una carga del efecto corona en el pararrayos (streamer discharge) que se transforme en un trazador conector (streamer to leader transition) que sea estable hasta su encuentro con el trazador descendente.
A1.3. Se llama “distancia de cebado” o “distancia disruptiva” Ds (`striking distance´), a la distancia que hay entre la punta del trazador negativo descendente por pasos del rayo nube–tierra y la punta del pararrayos en el momento (instante) en el cual sale un trazador ascendente conector exitoso (conecting leader) desde ese pararrayos y se produce el salto final de ambas descargas.
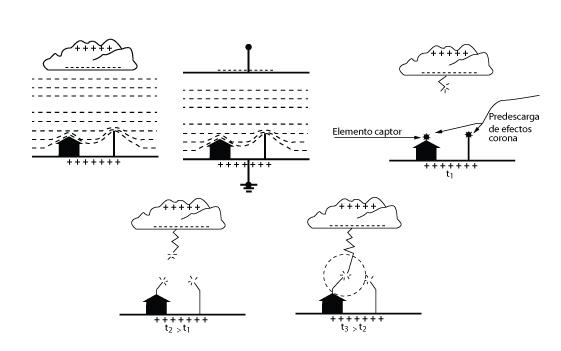
Figura A1. Proceso de descarga de un rayo a tierra (carga negativa en la nube). Adaptado de [5].
Nota: En el modelo electrogeométrico, el líder descendente debe considerarse vertical y sin ramificaciones.
Figura A1.b. Iniciación del trazador descendente (líder de pasos) en la nube tormentosa
(instante t1).
Figura A1.a. Intensificación del campo eléctrico
por los cuerpos terrestres. Analogía nube-tierra con un gran capacitor plano.
Figura A1.c. Competición de trazadores ascendentes y descendente (instantes t2 > t1).
Figura A1.d. Conexión entre líderes descendente y ascendente (instantes t3 > t2). El rayo cae en el pararrayos.
A2. Fundamentos de las protecciones contra los rayos [13]
Las protecciones contra rayos clásicas o convencionales se basan en el uso de pararrayos franklin (puntas franklin) y jaulas de Faraday (método de las mallas) en los cuales su efectividad depende de:
El desarrollo de una descarga por efecto corona en su/s punta/s.
La forma de una descarga conectora ascendente (streamer).
El desarrollo de un trazador ascendente estable (leader) como resultado de los campos eléctricos intensos creados por la proximidad del trazador descendente del rayo nube–tierra (downward leader).
A3. Trazadores descendentes y ascendentes. Proceso de interconexión, modelo electrométrico del rayo negativo descendente [5].
La figura A1 muestra los conceptos básicos del inicio de un rayo negativo descendente típico a tierra (aproximadamente, 90% de los casos). En la figura A1, se muestra la equivalencia aproximada entre el sistema de cargas nube-tierra y un capacitor. Se pueden observar las líneas de potencial deformadas por la presencia de los objetos terrestres, lo que provoca la intensificación del campo eléctrico creado por la nube tormentosa eléctrica.
Un líder de pasos o descarga escalonada o trazador descendente (figura A1.b) se ha originado en la parte de la carga negativa de la nube. En la figura A1.c, se muestran los dos tipos de trazadores que se producen en el proceso de descarga. Los trazadores ascendentes libran una especie de competencia por conectarse al trazador descendente. En la figura A1.d se ha producido la conexión. En el modelo electrogeométrico a la distancia OP (figura A1.e) se la denomina “distancia disruptiva” o “de cebado” (Ds). La distancia Ds se define como la distancia entre el objeto a ser impactado y la punta del líder de pasos, en el instante que se inicia la interconexión con el líder ascendente (ver A4.b).
A4. Las tres distancias (Di, Ds y Ra) vinculadas con el proceso del impacto de un rayo según el modelo matemático de Farouk A. Rizk [12]. (Ver figura A2).
a) La distancia Di es la distancia entre la punta superior Pi del trazador negativo descendente (nube-tierra) y la punta del pararrayos o de la estructura (o conductor colector de rayos) desde donde sale un trazador positivo ascendente continuo (es decir, un conector entre los dos trazadores). Esta distancia Di no se debe confundir con la distancia de cebado o distancia disruptiva Ds.
b) La distancia Ds es la distancia de cebado o distancia disruptiva, que se define como la distancia entre la estructura (o el pararrayos) y la punta inferior Ps del trazador negativo descendente en el punto crítico de encuentro entre los dos trazadores. Es en el punto Ps donde el trazador negativo descendente (o una de sus ramas) cambia abruptamente de orientación en un salto final dirigido hacia el trazador positivo ascendente conector.
c) El radio de atracción Ra del pararrayos (o estructura) es la máxima distancia radial que permite que ocurra un encuentro exitoso entre los dos trazadores (el negativo descendente nube-tierra y el positivo ascendente del pararrayos o de la estructura).
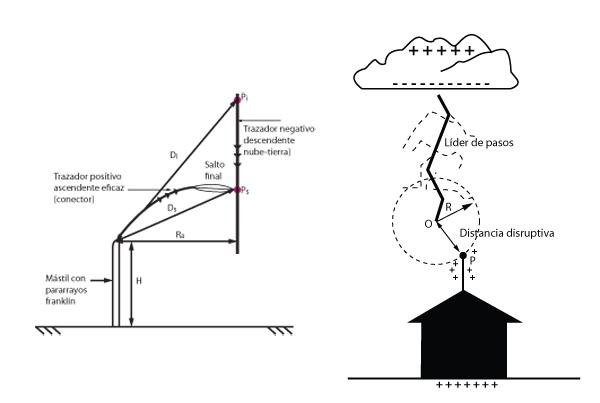
Figura A2. Esquema del proceso de un impacto de un rayo negativo descendente en un pararrayos franklin en un encuentro crítico entre dos trazadores correspondientes al máximo radio de atracción Ra según el modelo de Rizk [12].
Figura A2. Esquema del proceso de un impacto de un rayo negativo descendente en un pararrayos franklin en un encuentro crítico entre dos trazadores correspondientes al máximo radio de atracción Ra según el modelo de Rizk [12].
Referencias
Kindermann, Geraldo. Descargas atmosféricas, Sagra, Porto Alegre, 1992.
Horbath, Tibor. “Rolling sphere: Theory and application”. Paper 4.8 de 25º ICLP, Rodas, 2009.
Darveniza, Mat. “A modification to the rolling sphere method for positioning air terminals for lightning protection of building”, Paper 10 de 25º ICLP, Rodas, 2009.
Hartono, Zainal Abidin; Robiah, Ibrahim. “A method of identifying the lightning strike location on a structure” en Conferencia Internacional de Compatibilidad Electromagnética, Kuala Lumpur, 1995.
Reyna, Ángel. “Terminales captores de rayos y sus ángulos de protección: los ángulos de protección de un terminal captor de rayos en función de la altura h a un plano de referencia y del radio R de la esfera rodante”, en Ingeniería Eléctrica 175, Editores SRL, Buenos Aires, 2005.
Arcioni, Juan Carlos. La protección contra rayos de una punta Franklin interpretada según el método de la esfera rodante y un modelo probabilístico de angularidad vertical. (Apostilla: ver capítulos 9, 10 y 11 del trabajo citado en [9).
Arcioni, Juan Carlos. “Probables ángulos de caída de rayos a tierra con respecto a la vertical nube-tierra”, en Ingeniería Eléctrica, Editores SRL, Buenos Aires, octubre 2003.
Arcioni, Juan Carlos. “Como caen los rayos a tierra”, en Ingeniería Eléctrica 147, Editores SRL, Buenos Aires, julio 2001.
Arcioni, Juan Carlos. Giménez, Jorge Francisco. “Las esfera rodante” en Ingeniería Eléctrica, Editores SRL, Buenos Aires, mayo 2004.
Svedenik, N. “Rolling sphere: method or theory”, en Journal of Electrostatics 51-52, Elsevier Science, 2001.
Rakov, Vladimir. “Lightning phenomenology and parameters important for lightning protection”, en IX SPIDA, Brasil, 2007.
Rizk, Farouk A. M. “Modelling of lightning exposure of building and massive structures”, IEEE Trans. En Pw. Del. Vol. 24 Nº 4, Estados Unidos, octubre 2009.
Arcioni, Juan Carlos. Giménez, Jorge Francisco. “Breve reseña de los fenómenos físicos de los rayos (física del rayo) y la actuación de los pararrayos”, en Ingeniería Eléctrica, Editores SRL, Buenos Aires, octubre 2013.
Horvath, Tibor. “Standarization of lightning protection based on physics or the tradition”, en Journal of Electrostatics 60, 2004.
Arcioni, Juan Carlos. Giménez, Jorge Francisco. “Los mecanismos electrofísicos de impacto de un rayo negativo descendente de una nube tormentosa hacia tierra”, en Ingeniería Eléctrica, Editores SRL, Buenos Aires, 2013.
Briozzo, César. Simon, María. “Pararrayos no convencionales”, en 7º Encuentro de Energía, Potencia, Instrumentación y Medidas (EPIM), Montevideo, 2008.
Cooray, Vernon. Rakov, Vladimir. Theethayy, Nelson. “The lightning striking distance revisited”, en Journal of Electrostatics 65, noviembre 2006.
Arcioni, Juan Carlos. “Las funciones probabilísticas logaritmo-normales y sus representaciones gráficas: aplicaciones a la ingeniería de la protección contra rayos”, en Ingeniería Eléctrica, Editores SRL, Buenos Aires, junio 2004. |