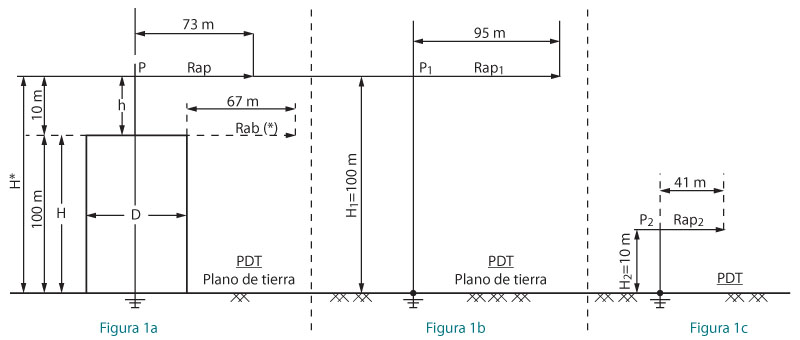
Figura 1a. Pararrayos P en un mástil en el centro del techo de un edificio cilíndrico de 100 metros de altura y 40 de diámetro. Rap es el radio de atracción del pararrayos P de 10 metros de altura sobre el techo. *Rab es el radio de atracción del borde del edificio, 67 metros para este caso. Nota: corriente presunta de 12 kAc Figura 1b. Pararrayos P1 de 110 metros de altura sobre el plano de tierra (solo y aislado). Rap1 es el radio de atracción de P1, de 110 metros de altura sobre el plano de tierra. Nota: corriente presunta de 12 kAc Figura 1c. Pararrayos P2 de 10 metros de altura sobre el plano de tierra (solo y aislado. Rap2 es el radio de atracción de P2, de 10 metros de altura sobre el plano de tierra. Nota: corriente presunta de 12 kAc
La estructura constructiva de los edificios interactúa con los rayos a tierra que descienden de las nubes en las tormentas eléctricas, trasladando cargas negativas de la nube a la tierra en el 90% de los casos hacia la superficie terrestre. Esa interacción entre los rayos descendentes negativos y los edificios que puedan impactar se manifiesta en los pararrayos del sistema de protección contra los rayos (SPCR) instalados para protegerlos, pero también se verifica en los bordes de las paredes, barandas metálicas, esquinas, y otros ángulos diedros y triedros, etc. que tengan los edificios afectados por los rayos.
Los radios de atracción de rayos de los pararrayos del sistema de protección contra los rayos y de las partes atractivas de los edificios (bordes, esquinas, etc.)
En “Anexo A” de esta nota técnica, repasamos los conceptos sobre pararrayos que los autores expusieron en Ingeniería Eléctrica N° 281 (octubre de 2013) y que ahora reproducen y completan con un ejemplo numérico en su nueva figura A3, dibujada a partir de los datos de Farouk Rizk (ver “Bibliografía”).
En la figura 1a, tenemos un edificio cilíndrico de 40 metros de diámetro y 100 de altura, con un pararrayos de 10 metros de altura en el centro del techo.
El radio de atracción del pararrayos es de aproximadamente 73 metros para una corriente presunta mayor o igual a 12 kAc de retorno a la nube de las cargas positivas (inducidas electrostáticamente hacia la tierra por el trazador negativo descendente desde la nube tormentosa eléctrica hacia el pararrayos).
Pero al mismo tiempo que se desarrollan desde el pararrayos los fenómenos electrofísicos que se representan matemáticamente por el radio “Rap”, también el borde de la pared del edificio “atrae” al mismo rayo que el pararrayos central, y así “aparece” el radio de atracción del borde “Rab”, igual a 67 metros. Es decir que todo ocurre como si el borde compitiese contra el pararrayos central del techo.
La distancia del borde al centro del edificio es el radio, para este caso, es de 20 metros. Entonces, el radio de atracción eficaz del borde puede ser de 97 metros con respecto al centro (Rab* = Rab + R = 67 m + 20 m = 97 m), que es mayor que el radio de atracción del pararrayos, que equivale a 73 metros.
Podemos decir que el pararrayos tiene una posible influencia desfavorable del borde del edificio que compite por la atracción de los rayos.
Un método original de Rizk
En la figura 1b, tenemos un pararrayos P1 de 110 metros de altura sobre el plano de tierra (ideal, horizontal, electroconductor perfecto). Vemos que el pararrayos P1 está solo y aislado de todos los cuerpos físicos circundantes (masas).
La altura del pararrayos P1 sobre el plano de tierra es de 100 más 10, 110 metros, es decir que para este caso, la altura es igual a 110 metros. Vemos que los pararrayos P y P1 tienen alturas iguales sobre el plano de tierra. También podemos comparar sus radios de atracción:
-
Pararrayos P: radio de atracción de 73 metros
-
Pararrayos P1: radio de atracción de 95 metros
Así podemos definir la relación entre los radios de atracción de un pararrayos P, con altura sobre el plano de tierra, y otro radio de atracción para el pararrayos P1, con altura sobre el plano de tierra, siendo ambos radios calculados para la misma corriente presunta de 12 kAc.
Entonces, obtenemos la relación RRA entre radios de atracción:
RRA = Rap/Rap1 = 73 m/95 m = 0,77 = 77%
Es decir, la proximidad del edificio a un pararrayos tiene un efecto significativo en la reducción de su radio de atracción con respecto al que tendría ese mismo pararrayos si estuviera solo y aislado para la misma altura total contra el plano de tierra e idéntica corriente presunta.
En la figura 1c, tenemos el pararrayos P2 de 10 metros de altura, siendo su radio de atracción igual a 41 metros para corriente presunta igual a 12 kA. Podemos comparar los pararrayos P2 y P1.
Comprobamos lo siguiente:
-
H1/H2 = 110 m/10 m = 11 veces
-
Rap2/Rap1 = 95 m/41 m = 2,32 veces
-
11/2,32 = 4,7 veces
Es decir, la diferencia entre radios es 4,7 veces menor que la diferencia entre alturas.
Ejemplo de un sistema de protección contra los rayos con cuatro (o seis) pararrayos P2 de dos metros de altura colocados al borde del edificio cilíndrico (100 metros de altura y 40 de diámetro)
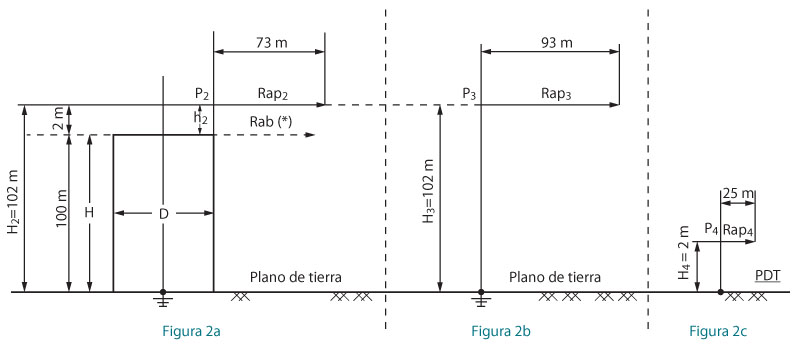
Figura 2a. Pararrayos P2 en un mástil del borde del techo de un edificio cilíndrico de 100 metros de altura y 40 de diámetro. Rap es el radio de atracción del pararrayos P2 de 2 metros de altura sobre el techo. *Rab es el radio de atracción del borde del edificio, 67 metros para este caso. Nota: corriente presunta de 12 kAc
Figura 2b. Pararrayos P3 de 102 metros de altura sobre el plano de tierra (solo y aislado). Rap3 es el radio de atracción de P2, de 100 metros de altura sobre el plano de tierra. Nota: corriente presunta de 12 kAc
Figura 2c. Pararrayos P4 de 2 metros de altura sobre el plano de tierra (solo y aislado). Rap4 es el radio de atracción de P4 , de 2 metros de altura sobre el plano de tierra. Nota: corriente presunta de 12 kAc
En la figura 2a tenemos que el pararrayos P2, de dos metros de altura con respecto al techo y de 102 metros con respecto al plano de tierra, tiene un radio de atracción de 73 metros para la corriente presunta de 12 kAc.
Este radio de atracción del pararrayos P2 es mayor que el radio de atracción de 67 metros del borde del edificio:
-
Rap2/Rab = 73 m/67 m = 1,09
-
RRA = Rap2/Rap33 = 73 m/93 m 0,78
Podemos concluir que estos pararrayos P2 colocados al borde del edificio pero conjuntamente a otros tres para completar cuatro (u otros cinco para totalizar seis) es decir, dispuestos formando un cuadrado (o hexágono) de pararrayos P2, todos colocados al borde del edificio cilíndrico, pueden formar un sistema de protección contra los rayos capaz de proteger el edificio, porque su relación radio de atracción del pararrayos/radio de atracción del borde es de 1,09, que es un 9% mayor que 1. Podemos notar que en este caso (figura 2), el efecto de atracción del borde del edificio (67 metros) complementa al efecto de atracción del pararrayos P2 (73 metros) colocado sobre dicho borde.
Radios de protección estimados para bordes (aristas) y para esquinas (ángulos diedros y triedros entre paredes y/o techos, etc.)
En el apartado que sigue resumimos los valores estimados por Rizk de las relaciones entre radios para el radio de atracción del borde (arista) RRAb y el de una esquina (ángulo diedro o triedro), RRA3, de un edificio de altura h sobre el plano de tierra que definimos así:
RRA = Rab(m)/Rap(m) y RRAe = Rae(m)/Rap(m)
“Rap(m)” es el radio de protección de un pararrayos esbelto (solo y aislado de otros cuerpos) y de la misma altura que el borde (arista) o la esquina (ángulo diedro o triedro de paredes y/o techos). La altura se mide con respecto al plano de tierra, y los radios de atracción se calculan para la misma corriente presunta (kAc) atraída por el rayo considerado.
Comparación entre las atracciones de los bordes y de las esquinas de un mismo edificio afectado por un rayo de corriente presunta
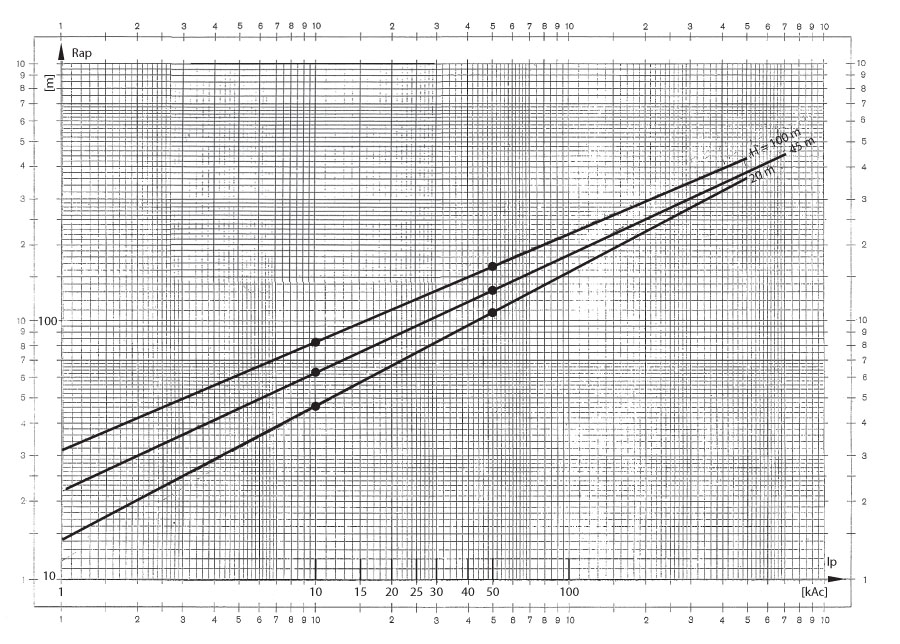 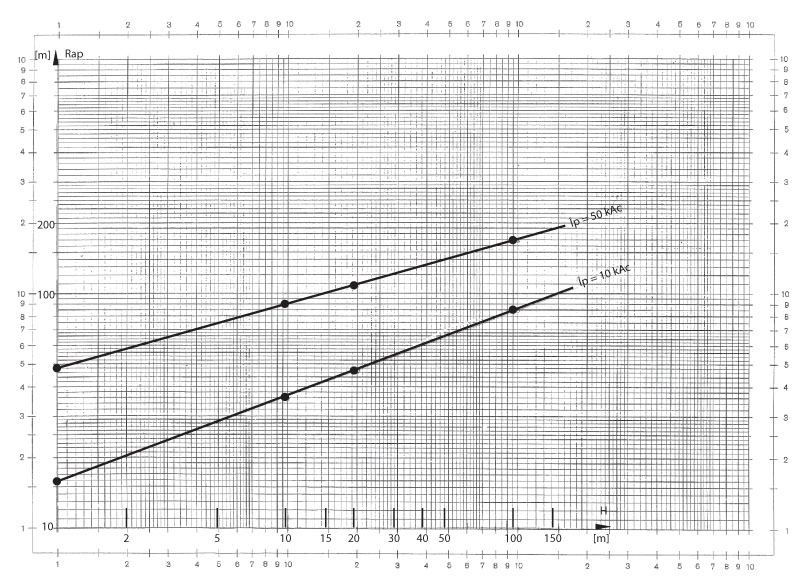
Figura 3. Radios de atracción para pararrayos esbeltos de alturas H sobre el plano de tierra (solos y aislados) en función de la corriente presunta del rayo atraído (Ip)
Figura 4. Radios de atracción para pararrayos esbeltos de alturas sobre el plano de tierra (solos y aislados) en función de la altura y para las dos corrientes presuntas de los rayos atraídos
Aplicamos las definiciones del apartado anterior, y así obtenemos las relaciones comparativas K siguientes:
Esquinas vs. bordes para la corriente presunta de 5 kAc:
K (e; b) = RRA2/RRAb = 80%/70% = 1,14 para h 20 m
K (e; b) = 80%/60% = 1,33 para h 100 m
Esquinas vs. bordes para la corriente presunta de 10 kAc:
K (e; b) = RRAe/RRAb = 85%/75% = 1,13
Conclusión: para la corriente presunta de 5 kAc, las esquinas son más vulnerables que los bordes a la acción de los rayos, particularmente para los edificios más altos (un 33% más para alturas de 100 metros contra un 13% más para alturas de 20 metros) pero para la corriente presunta de 10 kAc, las esquinas son más vulnerables que los bordes a cualquier altura del edificio.
Valores numéricos de los radios de atracción de los pararrayos (esbeltos, solos y aislados) en función de la corriente presunta de los rayos atraídos y de la altura sobre el plano de tierra
En la figura 3, representamos las tres funciones: “Rap = F(Ip; H)”, para alturas H de 20, 45 y 100 metros como parámetros.
En la figura 4, representamos las dos funciones “Rap = F(H; Ip)”para corriente presunta Ip de 5 o 50 kAc como parámetros.
Agradecimientos
Los autores de este artículo agradecen a Alejandro Menéndez y a Alejandra Bocchio por el trabajo editorial.
Bibliografía
-
Rakov, Vladimir (2007), “Lightning phenomenology and parameters important for lightning protection”, en IX SPIDA, Lectura 1, págs. 539 a 562, Brasil
-
Reyna, Ángel (2004), “Terminales captores de rayos y sus ángulos de protección”, en Ingeniería Eléctrica, Marzo-Abril 2004, Editores SRL, Buenos Aires
-
Rizk, Farouk A. M. (2009), “Modelling of lightning exposure of building and massive structures”, en IEEE Trans. En Pw. Del., Vol. 24, N° 4, octube 2009, Estados Unidos
Anexo A
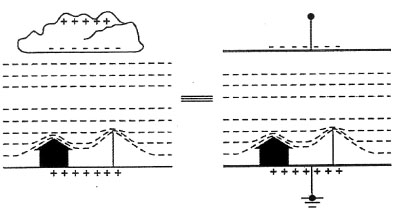 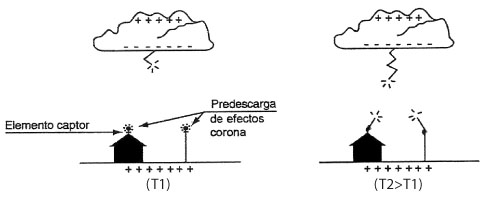
Figura A1. Proceso de descarga de un rayo a tierra
A1a. Intensificación del campo eléctrico por los cuerpos terrestres. Analogía nube-tierra con un gran capacitor plano
A1b. Iniciación del trazador descendente (líder de pasos) en la nube tormentosa (instante T1)
A1c. Competencia entre trazadores ascendente (instantes T2 > T1) (carga negativa en la nube). Adaptado de Ángel Reyna (ver “Bibliografía”). Nota: en el modelo electrogeométrico, el líder descendente debe considerarse vertical y sin ramificaciones
Actuación de los pararrayos, distancia de cebado o disruptiva, efectividad de las protecciones contra rayos
El impacto de un rayo en un pararrayos franklin ocurre mediante un trazador conector (conecting leader) que sale de la punta del pararrayos dirigida hacia el trazador descendente por pasos que están en el extremo del rayo nube tierra (downcoming stepped leader).
La salida exitosa del trazador conector desde el pararrayos hacia el rayo descendente requiere la formación de una descarga del efecto corona en el pararrayos (streamer discharge) que se transforme en un trazador conector (streamer to leader transition) que sea estable hasta su encuentro con el trazador descendente.
Se llama “distancia de cebado” o “distancia disruptiva” (striking distance) a la distancia que hay entre la punta del trazador negativo descendente por pasos del rayo nube-tierra y la punta del pararrayos en el momento (instante) en el cual sale un trazador ascendente conector exitoso (conecting leader) desde el pararrayos y se produce el salto final de ambas descargas.
Fundamentos de las protecciones contra los rayos
Las protecciones contra rayos clásicas o convencionales se basan en el uso del pararrayos franklin (puntas franklin) y de jaulas de faraday (método de las mallas) en los cuales su efectividad depende de:
-
El desarrollo de una descarga por efecto corona en su o sus puntas.
-
La formación de una descarga conectora ascendente (streamer).
-
El desarrollo de un trazador ascendente estable (leader) como resultado de los campos eléctricos intensos creados por la proximidad del trazador descendente del rayo nube-tierra (downward leader).
Trazadores descendentes y ascendentes. Proceso de conexión. Modelo electrogeométrico del rayo negativo descendente
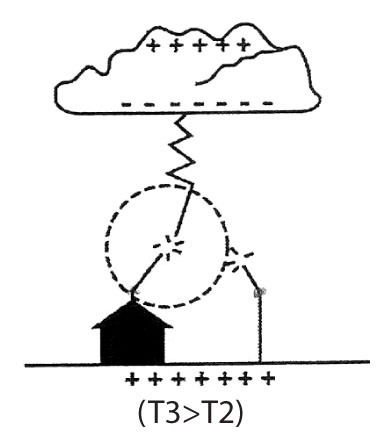 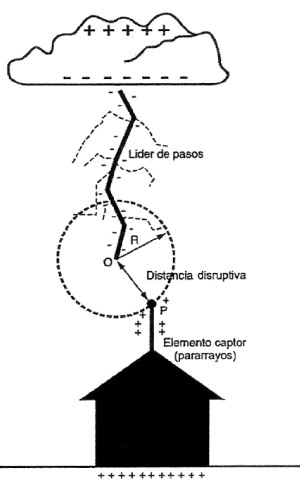
A1d. Conexión exitosa entre los líderes descendente y ascendente (instantes T3 > T2). El rayo cae en el pararrayos
A1e. Distancia disruptiva ds = R = 10 I2/3 (m; kAc)
La figura A1 muestra los conceptos básicos del inicio de un rayo negativo descendente típico a tierra (aproximadamente, 90% de los casos). Se muestra la equivalencia aproximada entre el sistema de cargas nube-tierra y un capacitor. Se pueden observar las líneas de potencial deformadas por la presencia de los objetos terrestres, lo que provoca la intensificación del campo eléctrico creado por la nube tormentosa eléctrica.
Un líder de pasos o descarga escalonada o trazador descendente (figura A1b) se ha originado en la parte de la carga negativa de la nube. En la figura A1c, se muestran los dos tipos de trazadores que se producen durante el proceso de descarga. Los trazadores ascendentes libran una especie de competencia por conectarse al trazador descendente. En la figura A1d se ha producido la conexión. En el modelo electrogeométrico a la distancia OP (figura A1e) se la denomina “distancia disruptiva” o “de cebado” (ds). La distancia ds se define como la distancia entre el objeto a ser impactado y la punta del líder de pasos, en el instante en que se inicia la conexión del líder ascendente.
Las tres distancias (di, ds y Ra) vinculadas con el proceso del impacto de un rayo según el modelo matemático de Rizk
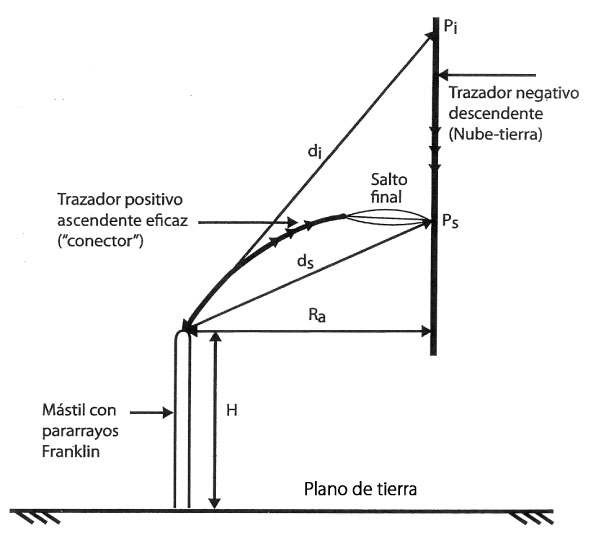
Figura A2. Esquema del proceso de un impacto de un rayo negativo descendente a un pararrayos franklin en un encuentro crítico entre dos trazadores correspondiente al máximo radio de atracción según el modelo de Rizk
(Ver las figuras A2 y A3). La distancia di es la distancia entre la punta superior Pi del trazador negativo descendente (nube-tierra) y la punta del pararrayos o de la estructura (o conductor colector de rayos) desde donde sale un trazador positivo ascendente continuo (es decir, un conector entre los dos trazadores). Esta distancia di no se debe confundir con la distancia de cebado o distancia disruptiva ds.
La distancia ds es la distancia de cebado o distancia disruptiva, que se define como la distancia entre la estructura (o el pararrayos) y la punta inferior Ps del trazador negativo descendente en el punto crítico de encuentro entre los dos trazadores. Es en este punto Ps donde el trazador negativo descendente (o una de sus ramas) cambia abruptamente de orientación en un salto final dirigido hacia el trazador positivo ascendente conector.
El radio de atracción del pararrayos (o estructura) es la máxima distancia radial que permite que ocurra un encuentro exitoso entre los dos trazadores (el negativo descendente nube-tierra y el positivo ascendente del pararrayos o estructura).
En la figura A3, completamos a la figura A2 con un ejemplo numérico que dibujamos con los datos de Rizk.
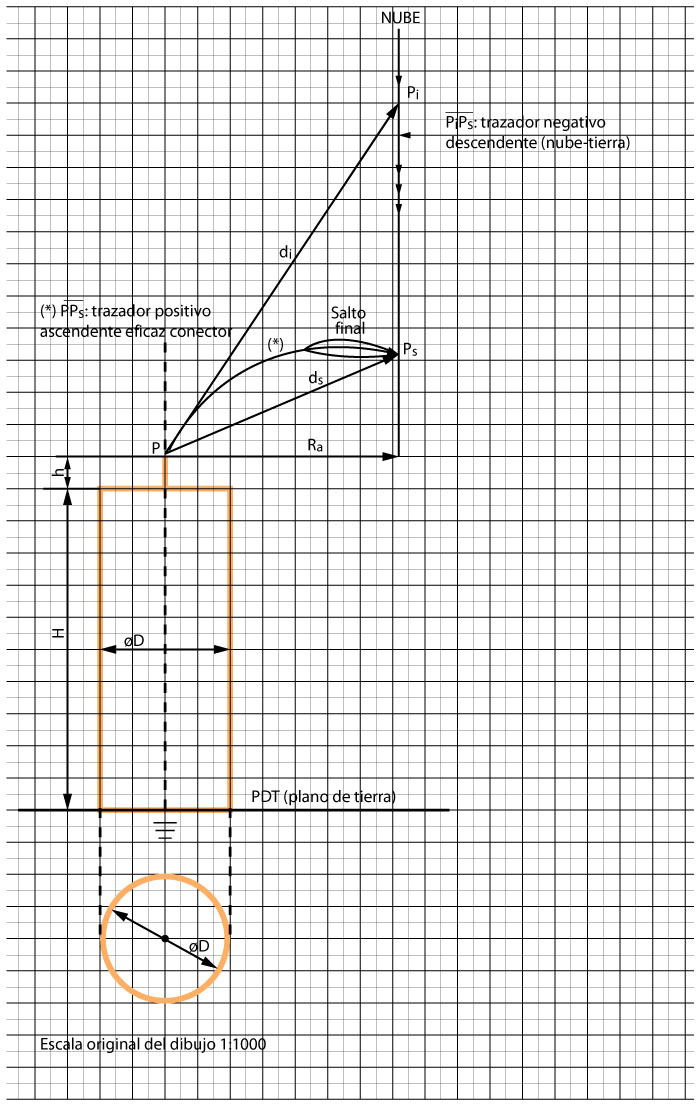
Figura A3. Esquema del proceso de impacto de un rayo negativo descendente PiPs en un pararrayos P sobre un edificio cilíndrico Datos numéricos:
• Edificio cilíndrico: 100 metros de altura y 40 de diámetro
• Pararrayos P en el centro del techo de 10 metros del altura
• Corriente de retorno presunta de 12 kAc
• Distancias: di de 133 metros; ds, 77 metros, y Ra de 73 metros
• Valor gráfico calculado: PiPs 80 m
|