|
Las distancias a las que dos o más pararrayos deben estar separados entre sí y con respecto a otros cuerpos u objetos metálicos o árboles cercanos tienen una notable influencia en su probable actuación durante las tormentas eléctricas en la protección contra rayos de edificios y estructuras. En esta nota técnica, los autores tratan de presentar algunos criterios que pueden ayudar en la instalación de los sistemas de protección contra rayos (SPCR) mediante pararrayos normalizados (normas argentinas IRAM 2428 e IRAM 2426).
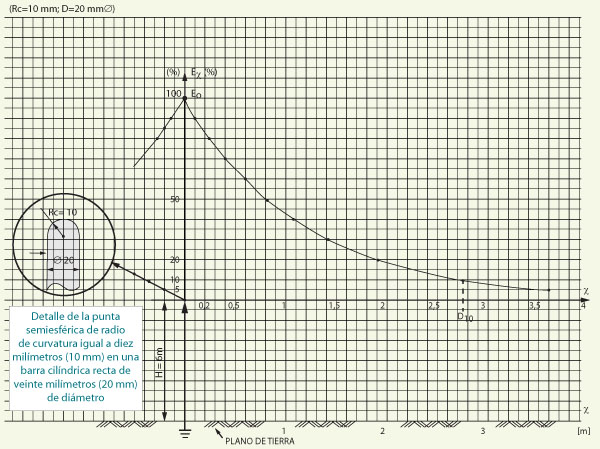
Figura 1. Campo electric –Ex (%) – estimado para una punta franklin de seis metros de altura y radio de curvature de diez milímetros (10 mm) en la punta, en función de las distancias x a la punta medida sobre el plano de tierra. El porcentaje Ex (%) se refiere al valor máximo de cien por ciento (100%) para X igual a cero metros. Nota: Ex ≅ E0 exp (-Ax).
Una idea de los campos eléctricos de una punta roma franklin sola y acompañada por otra igual
En la figura 1, representamos el campo eléctrico –Ex (%)– estimado para una punta de un pararrayos franklin de seis metros (6 m) de altura y radio de curvatura (Rc) en la punta de diez milímetros (10 mm), dibujado en función de la distancia x normal al eje de la punta del pararrayos medida sobre el plano de tierra donde está instalada la punta sola y aislada.
Este campo eléctrico lo producen las nubes tormentosas electrizantes situadas muy arriba del suelo donde está ubicada la punta, que consideramos que está sola y aislada de todos los otros cuerpos materiales que puedan rodearla y así afectan la distribución espacial del campo eléctrico.
Si se instalan dos puntas de pararrayos franklin iguales A y B (figura 2), la distancia entre ellos, sobre el plano de tierra, debe tener un valor tal que permita que tanto A como B actúen con la mayor independencia electrostática y electromagnética posible entre ellos.
Hemos dibujado en la figura 2 el campo eléctrico estimado de A de izquierda a derecha y el campo eléctrico B de derecha a izquierda. Hemos considerado que ambos campos parten de sus máximos de cien por ciento (100%) de cada uno y decrecen hasta que alcanzan un valor de diez por ciento (10%) aproximadamente, que suponemos que ocurre alrededor de la mitad de la distancia. Cada diez por ciento (10%) del campo eléctrico tiene lugar a la respectiva distancia D10, medidas desde la punta A y de la punta B sobre el eje X perpendicular a los ejes de los pararrayos iguales A y B.
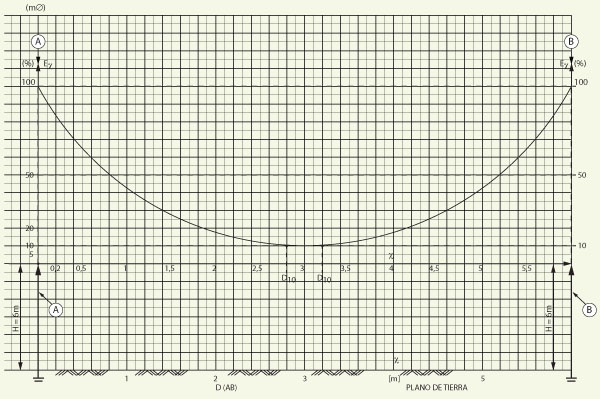
Figura 2. Campo electric – Ex (%) – entre los pararrayos Franklin A y B (de seis metros de altura y diez milímetros de radio de curvatura) colocados sobre el plano de tierra a una distancia de seis metros entre A y B.
La distancia D10 en los pararrayos franklin
Los autores Gerard Berger y Ramzi Hadaji presentaron en su conferencia de la V SIPDA, en 1999 en Brasil, la siguiente fórmula:
D = 1,6 H0,77 Rc0,27
en la que D es igual a D10, Rc y H están medidas (cantidades) en metros, siendo:
-
D (D10): la distancia en que el campo eléctrico de la punta franklin (Rc; H) retorna o vuelve al valor de un diez por ciento (10%) de su máximo campo ambiental tormentoso (cien por ciento –100%– en la punta).
-
Rc: radio de curvatura de la punta.
-
H: altura de la punta sobre el plano de referencia (terraza, tierra, techo, etcétera).
En la figura 3 representamos la función:
D10 = 1,6 H0,77 Rc0,27

Figura 3. Distancias D10 = 1,6 H0,77 Rc 0,27 en las puntas romas de radio de curvature (milímetros) y altura (metros) sobre el plano de referencia (tierra, techo, terraza, etcétera).
Las unidades de distancia y altura expresadas en metros y radio de curvatura en milímetros, por lo que si tenemos los valores siguientes para esta última: 1, 5, 10, 30, 50, 80, 500 y 1.000, las expresaremos en metros (0,00,1, 0,005, 0,010, etcétera) para aplicarlas en la fórmula.
En las figuras 1 y 2 hemos adoptado para la distancia el valor de 2,8 metros según las experiencias del investigador estadounidense Charles Moore para las puntas romas de diez milímetros (10 mm) de radio de curvatura y seis metros (6 m) de altura, con una “esbeltez” de seiscientos milímetros (600 mm), obtenidos de dividir la altura sobre el radio de curvatura (6.000 mm / 10 mm).
La fórmula de Berger antes citada nos da una distancia de 1,83 metros para estos valores de radio de curvatura y altura.
Podemos calcular la relación distancia sobre la esbeltez, lo que nos da 1,53 metros y así surge el criterio práctico siguiente: “Aumentar en un cincuenta por ciento (50%) como mínimo los valores de distancia D10 calculados en la fórmula para la punta franklin roma (ver figura 3) considerando las experiencias prácticas de Moore (ver “Las puntas agudas y romas de los pararrayos franklin y su efecto captor de los rayos a tierra” en Ingeniería Eléctrica 310, junio de 2016).
Otro criterio práctico: entre dos pararrayos A y B de igual altura sobre el plano de referencia, se recomienda que la distancia entre sus ejes sea igual o mayor a su altura. Si son de alturas diferentes, se recomienda tomar el promedio de alturas como mínimo. Si hay tres pararrayos, se puede aplicar tres veces el criterio anterior, así: entre A y B, B y C, A y C, es decir, de dos en dos pararrayos en el orden A, B, C.
 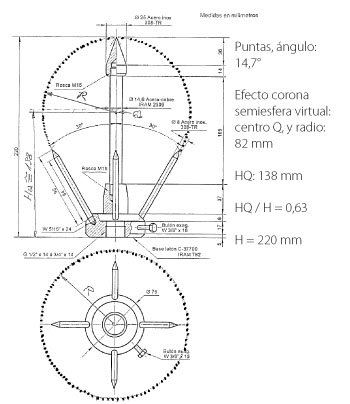
Figura 4. Pararrayos de cinco puntas (figures A1 y A2 de la Norma IRAM 2428:2002) con el agregado de la semiesfera virtual del efecto corona a cada modelo (dibujada en la línea punteda) | Figura 5. Pararrayos de cinco puntas para el extremo del mástil del modelo B1 de IRAM 2428:2002 con el agregado de la semiesfera virtual del efecto corona dibujada en línea punteada
Los pararrayos franklin de cinco puntas (agudas no romas)
Tal como podemos apreciar en las figuras 4 y 5, estos pararrayos disponen de una punta aguda central más larga que las otras cuatro puntas laterales iguales entre sí y dispuestas simétricamente alrededor de la punta larga central con agudos de inclinación de treinta, cuarenta o cincuenta grados (30, 40 o 50°) según los modelos (B2, A1 y A2 de la Norma IRAM 2428:2002).
Por la experiencia histórica argentina que los autores verbalmente obtuvieron de sus colegas: estos pararrayos de cinco puntas (cuatro más una –4 + 1–) han “atraído” rayos en cualquiera de sus puntas. Así quedó como recuerdo para un museo técnico un pararrayos de cinco puntas que “perdió” una de sus puntas laterales que fue totalmente fundida y vaporizada por un rayo (por su trazador ascendente positivo tierra-nube con la corriente de retorno Ip).
Para los autores, estos pararrayos de cinco puntas se comportan como si esas cinco puntas determinaran una semiesfera virtual de efecto corona. Dicha semiesfera virtual de efecto corona ocurre siempre antes del impacto de un rayo al pararrayos de cinco puntas porque es necesario un efecto corona de valor y duración adecuadas para que actúe el pararrayos.
Posible equivalencia del pararrayos de cinco puntas a una punta roma virtual: los autores consideran que el radio de curvatura de la punta roma virtual es el radio de la semiesfera virtual de efecto corona (figuras 4 y 5).
Ejemplo numérico: el radio de las tres semiesferas virtuales de efecto corona dibujadas (figuras 4 y 5) es de un valor de ochenta y cuatro milímetros (84 mm) en promedio (media aritmética).
Entonces, para un pararrayos de cinco puntas de radio de curvatura de ochenta y cuatro milímetros (84 mm) y seis metros (6 m) de altura, resultará que la distancia D10 será de 3,3 metros. Adoptando D*10 = 1,5 D10 = 4,9 resulta que se verifica el criterio de separación antes expuesto.
La “esbeltez” de esta punta roma virtual es una esbeltez virtual de valor de setenta y un milímetros (71 mm), proveniente de dividir la altura sobre radio de curvatura (6.000 mm / 84 mm 71), que representa un doce por ciento (12%) de la esbeltez de la punta de Moore.
Bibliografía
Beeren, Hans von, Técnica de alta tensión”, en La escuela del técnico electricista, Tomo XII, Labor, Buenos Aires, 1946.
Berger, Gerard; Hadaji, Ramzi, “Lightning attachment physics – Experiments and modelling”, conferencia en V SIPDA, San Pablo, 17 al 21 de mayo de 1999.
Faircloth, Daniel Clarke, Lightning protection of buildings using active finials, Instituto de Ciencia y Tecnología, Universidad de Manchester, Manchester, 1996.
Kopecky, Vojtech, “Lightning protection systems with ESE devices under scrutiny”, reimpresión de Elektropraktiker, Berlin 64, 2010.
Moore, C.; Aulich, G.; Rison, W., “Responses of lightning rods to nearby lightning”. Conferencia internacional sobre rayos y electricidad estática, Seattle, Washington. Warrendale, Pensilvania, 1 al 13 de septiembre de 2001,
Rose, A. Jean; Penel, Charles, “Ionization des gaz-Pouvoir des pointes”, en L'Electrostatique, la Revue du Palais de la Decouverte, número especial 6, París, 1976.
Sidik, M. et alles, Study on the effectiveness of lightning rod tips in capturing lightning leaders, Universidades de Malasia e Indonesia, Springer Verlag, Berlín, Heidelberg, 2013. |